设复数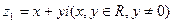 ,复数
,复数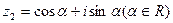 ,且
,且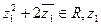 在复平面上所对应点在直线
在复平面上所对应点在直线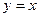 上,求
上,求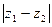 的取值范围。
的取值范围。
已知三点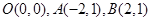 及曲线
及曲线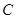 上任意一点
上任意一点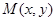 ,满足
,满足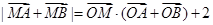 ,求曲线
,求曲线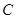 的方程,并写出其焦点坐标.
的方程,并写出其焦点坐标.
已知椭圆与双曲线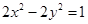 共焦点,且过(
共焦点,且过(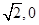 )
)
(1)求椭圆的标准方程.
(2)求斜率为2的椭圆的一组平行弦的中点轨迹方程;
已知命题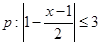 ;
;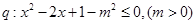 若
若 是
是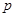 的充分非必要条件,试求实数
的充分非必要条件,试求实数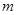 的取值范围.
的取值范围.
(本小题满分12分)已知平面上一定点 和一定直线
和一定直线
 为该平面上一动点,作
为该平面上一动点,作 ,垂足为
,垂足为 ,且
,且
(1)问点 在什么曲线上?并求出该曲线的方程;
在什么曲线上?并求出该曲线的方程;
(2)设直线 与(1)中的曲线交于不同的两点
与(1)中的曲线交于不同的两点 ,是否存在实数
,是否存在实数 ,使得以线段
,使得以线段 为直径的圆经过点
为直径的圆经过点 ?若存在,求出
?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知中心在原点的椭圆 的左焦点
的左焦点 ,右顶点
,右顶点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)斜率为 的直线
的直线  与椭圆
与椭圆 交于
交于 两点,求弦长
两点,求弦长 的最大值及此时
的最大值及此时 的直线方程.
的直线方程.