设函数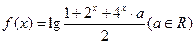 ,如果当
,如果当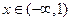 时
时 总有意义,
总有意义,
求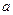 的取值范围.
的取值范围.
设函数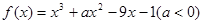 ,且曲线
,且曲线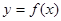 斜率最小的切线与直线
斜率最小的切线与直线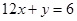 平行.
平行.
求:(1)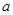 的值;
的值;
(2)函数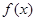 的单调区间.
的单调区间.
已知向量 ,
,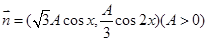 ,函数
,函数 的最大值为6.
的最大值为6.
(1)求 ;
;
(2)将函数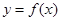 的图象向左平移
的图象向左平移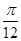 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的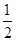 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数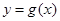 的图象.求
的图象.求 在
在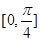 上的值域.
上的值域.
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当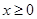 时,
时, ,
,
(1)当 时,求不等式
时,求不等式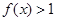 的解集;
的解集;
(2)若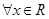 ,
,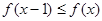 ,求实数
,求实数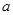 的取值范围.
的取值范围.
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为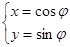 (
(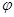 为参数),曲线
为参数),曲线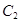 的参数方程为
的参数方程为 为参数),在以
为参数),在以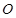 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线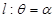 与
与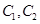 各有一个交点.当
各有一个交点.当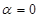 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当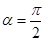 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明 是什么曲线,并求出
是什么曲线,并求出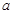 与
与 的值;
的值;
(2)设当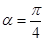 时,
时,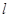 与
与 的交点分别为
的交点分别为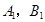 ,当
,当 时,
时,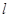 与
与 的交点为
的交点为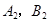 ,求四边形
,求四边形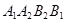 的面积.
的面积.
如图,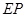 交圆于
交圆于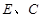 两点,
两点,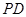 切圆于
切圆于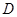 ,
, 为
为 上一点,且
上一点,且 ,连接
,连接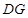 并延长交圆于点
并延长交圆于点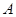 ,作弦
,作弦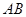 垂直
垂直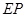 ,垂足为
,垂足为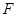 .
.
(1)求证: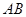 为圆的直径;
为圆的直径;
(2)若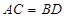 ,求证:
,求证: .
.