在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为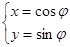 (
(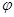 为参数),曲线
为参数),曲线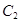 的参数方程为
的参数方程为 为参数),在以
为参数),在以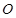 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线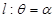 与
与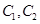 各有一个交点.当
各有一个交点.当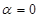 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当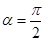 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明 是什么曲线,并求出
是什么曲线,并求出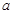 与
与 的值;
的值;
(2)设当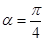 时,
时,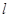 与
与 的交点分别为
的交点分别为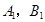 ,当
,当 时,
时,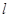 与
与 的交点为
的交点为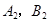 ,求四边形
,求四边形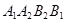 的面积.
的面积.
已知点(1,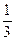 )是函数
)是函数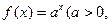 且
且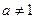 )的图象上一点,等比数列
)的图象上一点,等比数列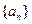 的前项和为
的前项和为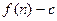 ,数列
,数列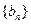
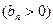 的首项为,且前项和
的首项为,且前项和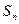 满足
满足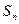 -
-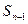 =
=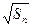 +
+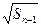 (
(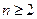 ).
).
(1)求数列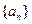 和
和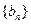 的通项公式;
的通项公式;
(2)若数列{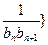 前项和为
前项和为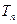 ,问
,问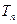 >
>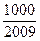 的最小正整数是多少?
的最小正整数是多少?
如图,在直角梯形 中,
中,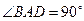 ,
,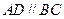 ,
,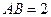 ,
,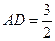 ,
,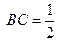 ,椭圆以
,椭圆以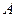 、
、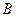 为焦点且经过点
为焦点且经过点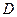 .
.
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(Ⅱ)以该椭圆的长轴为直径作圆,判断点C与该圆的位置关系。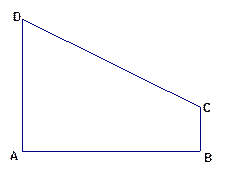
在等差数列 中,
中, ,
,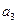 与
与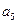 的一个等比中项为
的一个等比中项为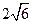 。
。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的通项
的通项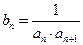 ,求数列
,求数列 的前
的前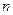 项和
项和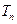 。
。
下表为某体育训练队跳高、跳远成绩的分布,共有队员40人,成绩分为1~5五个档次。例如表中所示跳高成绩为4分,跳远成绩为2分的队员为5人.将全部队员的姓名卡混合在一起,任取一张,该卡片队员的跳高成绩为x分,跳远成绩为y分.
⑴求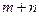 的值;
的值;
⑵求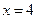 的概率及
的概率及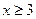 且
且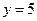 的概率.
的概率.
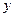 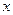 |
跳远 |
|||||
| 5 |
4 |
3 |
2 |
1 |
||
跳 高 |
5 |
1 |
3 |
1 |
0 |
1 |
| 4 |
1 |
0 |
2 |
5 |
1 |
|
| 3 |
2 |
1 |
0 |
4 |
3 |
|
| 2 |
1 |
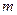 |
6 |
0 |
 |
|
| 1 |
0 |
0 |
1 |
1 |
3 |
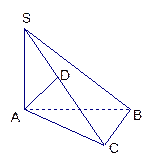
已知 中∠ACB=90°,SA⊥面ABC,AD⊥SC于D,
中∠ACB=90°,SA⊥面ABC,AD⊥SC于D,
求证: AD⊥面SBC;