已知曲线 的参数方程为
的参数方程为 为参数,
为参数, ),直线
),直线 在参数方程是
在参数方程是 为参数),曲线
为参数),曲线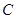 与直线
与直线 有一个公共点在
有一个公共点在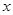 轴上,以坐标原点为极点,
轴上,以坐标原点为极点,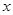 轴的正半轴为极轴建立极坐标系。
轴的正半轴为极轴建立极坐标系。
(1)求曲线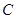 的普通方程;
的普通方程;
(2)若点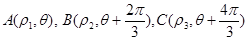 在曲线
在曲线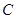 上,求
上,求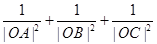 的值。
的值。
有一块边长为4的正方形钢板,现对其切割、焊接成一个长方体无盖容器(切、焊损耗忽略不计)。有人应用数学知识作如下设计:在钢板的四个角处各切去一个全等的小正方形,剩余部分围成一个长方体,该长方体的高是小正方形的边长。
(1)请你求出这种切割、焊接而成的长方体容器的最大容积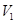 ;
;
(2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积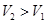 。
。
设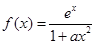 ,其中a为正实数。
,其中a为正实数。
(1)当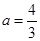 时,求
时,求 的极值点;
的极值点;
(2)若 在R不是单调函数,求a的取值范围。
在R不是单调函数,求a的取值范围。
已知数列 满足
满足 ,且
,且 。
。
(1)求 。
。
(2)猜想数列 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。
(1)证明: ;
;
(2)已知 ,求证:
,求证: 。
。
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球;乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,
①摸出3个白球的概率;
②获奖的概率;
(2)求在两次游戏中获奖次数 的分布列及数学期望
的分布列及数学期望 .
.