某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如下(单位:cm)
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值;
(2)在身高为140—160的学生中任选2个,求至少有一人的身高在150—160之间的概率.
已知数列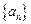 满足
满足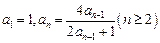 .
.
(1)求数列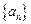 的通项公式;
的通项公式;
(2)证明不等式: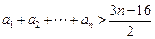 .
.
已知数列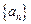 满足
满足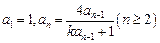 .
.
(1)求数列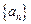 的通项公式;
的通项公式;
(2)当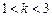 时,证明不等式:
时,证明不等式: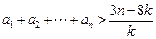 .
.
设函数f(x)= 在[1+,∞
在[1+,∞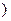 上为增函数.
上为增函数.
(1)求正实数a的取值范围.
(2)若a=1,求征: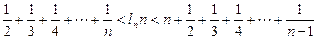 (n∈N*且n≥2)
(n∈N*且n≥2)
已知正项数列 的前
的前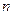 项和
项和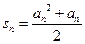 ,
,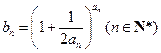 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)定理:若函数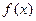 在区间D上是凹函数,且
在区间D上是凹函数,且 存在,则当
存在,则当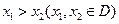 时,总有
时,总有 .请根据上述定理,且已知函数
.请根据上述定理,且已知函数 是
是 上的凹函数,判断
上的凹函数,判断 与
与 的大小;
的大小;
(Ⅲ)求证: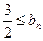 .
.
已知 函数f(x)=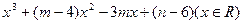 的图像关于原点对称,其中m,n为实常数。
的图像关于原点对称,其中m,n为实常数。
(1)求m , n的值;
(2)试用单调性的定义证明:f (x) 在区间[-2, 2] 上是单调函数;
(3)[理科做] 当-2≤x≤2 时,不等式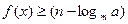 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。