如图1,在直角梯形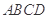 中,
中,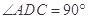 ,
, ,
, , 点
, 点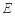 为
为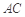 中点.将
中点.将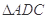 沿
沿 折起, 使平面
折起, 使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
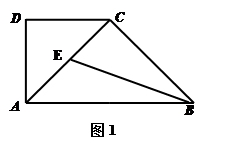
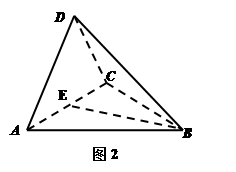
(1)在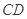 上找一点
上找一点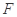 ,使
,使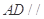 平面
平面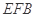 ;
;
(2)求点 到平面
到平面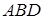 的距离.
的距离.
(本小题满分12分)如图,四棱锥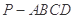 中,
中,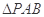 是正三角形,四边形
是正三角形,四边形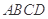 是矩形,且平面
是矩形,且平面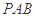
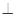 平面
平面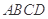 ,
,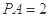 ,
,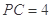 .
.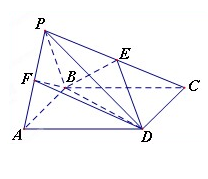
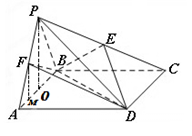
(Ⅰ)若点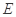 是
是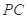 的中点,求证:
的中点,求证: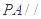 平面
平面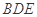 ;
;
(Ⅱ)若点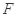 在线段
在线段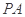 上,且
上,且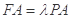 ,当三棱锥
,当三棱锥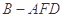 的体积为
的体积为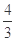 时,求实数
时,求实数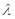 的值.
的值.
(本小题满分12分)如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.
(1)学校所有走读生早上上学所需要的平均时间约是多少分钟?
(2)根据调查,距离学校500米以内的走读生上学时间不超过10分钟,距离学校1000米以内的走读生上学时间不超过20分钟.那么,距离学校500米以内的走读生和距离学校1000米以上的走读生所占全校走读生的百分率各是多少?
(本小题12分)已知函数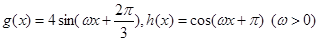 .
.
(Ⅰ)当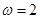 时,把
时,把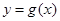 的图像向右平移
的图像向右平移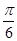 个单位得到函数
个单位得到函数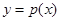 的图像,求函数
的图像,求函数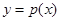 的图像的对称中心坐标;
的图像的对称中心坐标;
(Ⅱ)设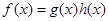 ,若
,若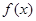 的图象与直线
的图象与直线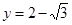 的相邻两个交点之间的距离为π,求
的相邻两个交点之间的距离为π,求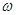 的值,并求函数
的值,并求函数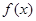 的单调递增区间.
的单调递增区间.
(本小题满分13分)已知椭圆 (
( )经过点
)经过点 ,离心率为
,离心率为 ,动点
,动点 (
( ).
).
(1)求椭圆的标准方程;
(2)求以 (
( 为坐标原点)为直径且被直线
为坐标原点)为直径且被直线 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;
(3)设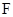 是椭圆的右焦点,过点
是椭圆的右焦点,过点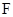 作
作 的垂线与以
的垂线与以 为直径的圆交于点
为直径的圆交于点 ,证明线段
,证明线段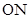 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
已知等差数列 的公差不为零,
的公差不为零, ,等比数列
,等比数列 的前3项满足
的前3项满足 .
.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)设 …
… ,是否存在最大整数
,是否存在最大整数 ,使对任意的
,使对任意的 ,均有
,均有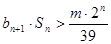 总成立?若存在,求出
总成立?若存在,求出 的值;若不存在,请说明理由
的值;若不存在,请说明理由