(本题13分)
向量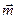 =(
=(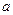 +1,
+1, ),
),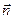 =(1,4cos(x
=(1,4cos(x +)),设函数
+)),设函数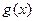 =
= (
(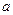 ∈R,且
∈R,且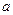 为常数).
为常数).
(1)若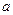 为任意实数,求
为任意实数,求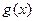 的最小正周期;
的最小正周期;
(2)若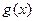 在[0,)上的最大值与最小值之和为7,求
在[0,)上的最大值与最小值之和为7,求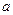 的值.
的值.
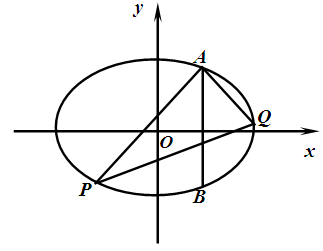
如图,两条相交线段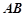 、
、 的四个端点都在椭圆
的四个端点都在椭圆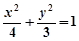 上,其中,直线
上,其中,直线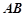 的方程为
的方程为 ,直线
,直线 的方程为
的方程为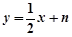 .
.
(1)若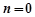 ,
,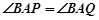 ,求
,求 的值;
的值;
(2)探究:是否存在常数 ,当
,当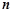 变化时,恒有
变化时,恒有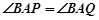 ?
?
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A,B,M为抛物线弧AB上的动点.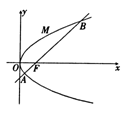
(1)若|AB|=8,求抛物线的方程;
(2)求 的最大值
的最大值
设定圆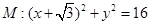 ,动圆
,动圆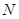 过点
过点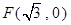 且与圆
且与圆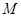 相切,记动圆
相切,记动圆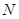 圆心
圆心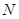 的轨迹为
的轨迹为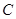 .
.
(1)求轨迹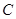 的方程;
的方程;
(2)已知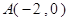 ,过定点
,过定点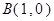 的动直线
的动直线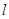 交轨迹
交轨迹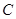 于
于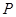 、
、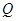 两点,
两点, 的外心为
的外心为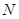 .若直线
.若直线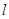 的斜率为
的斜率为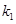 ,直线
,直线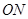 的斜率为
的斜率为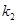 ,求证:
,求证: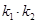 为定值.
为定值.
已知椭圆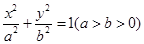 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率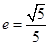 ,直线
,直线 交椭圆于M,N两点。
交椭圆于M,N两点。
(1)若直线 的方程为
的方程为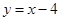 ,求弦MN的长;
,求弦MN的长;
(2)如果△BMN的重心恰好为椭圆的右焦点F,求直线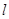 方程的一般式。
方程的一般式。
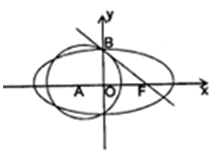
如图,点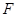 为椭圆
为椭圆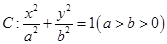 右焦点,圆
右焦点,圆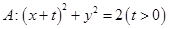 与椭圆
与椭圆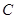 的一个公共点为
的一个公共点为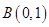 ,且直线
,且直线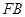 与圆
与圆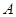 相切与点
相切与点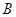 。
。
(1)求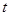 的值及椭圆
的值及椭圆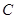 的标准方程;
的标准方程;
(2)设动点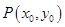 满足
满足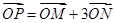 ,其中
,其中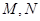 是椭圆
是椭圆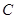 上的点,
上的点,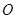 为原点,直线
为原点,直线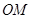 与
与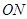 的斜率之积为
的斜率之积为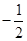 ,求证:
,求证: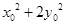 为定值。
为定值。