如图所示，均可视为质点的三个物体A、B、C穿在竖直固定的光滑绝缘细线上，A与B紧靠在一起（但不粘连），C紧贴着绝缘地板，质量分别为MA=2.32kg，MB=0.20kg，MC=2.00kg，其中A不带电，B、C的带电量分别为qB = +4.0×10-5c，qC =+7.0×10-5c，且电量都保持不变，开始时三个物体均静止。现给物体A施加一个竖直向上的力F，若使A由静止开始向上作加速度大小为a=4.0m/s2的匀加速直线运动，则开始需给物体A施加一个竖直向上的变力F，经时间t后，F变为恒力。已知g=10m/s2，静电力恒量k=9×109N·m2/c2，求：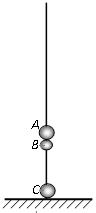
（1）静止时B与C之间的距离；
（2）时间t的大小；
（3）在时间t内，若变力F做的功WF=53.36J，则B所受的电场力对B做的功为多大？
如图所示，长为L (L=ab=dc)，高为L(L=bc=ad)的矩形区域abcd内存在着匀强电场。电量为q、质量为m、初速度为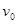
的带电粒子从a点沿ab方向进入电场，不计粒子重力。求：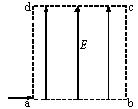
（1）若粒子从c点离开电场，求电场强度的大小；
（2）若粒子从bc边某处离开电场时速度为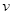
，求电场强度的大小。
如图所示，竖直面内有一绝缘轨道，AB部分是光滑的四分之一圆弧，圆弧半径R=0.5m，B处切线水平，BC部分为水平粗糙直轨道。有一个带负电的小滑块（可视为质点）从A点由静止开始下滑，运动到直轨道上的P处刚好停住。小滑块的质量m=1kg，带电量为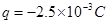
保持不变，滑块小轨道BC部分间的动摩擦因数为μ=0.2，整个空间存在水平向右的匀强电场，电场强度大小为E=4.0×102N/C.（g=10m/s2）
（1）求滑块到达B点瞬间的速度大小
（2）求滑块到达B点瞬间对轨道的压力大小。
（3）求BP间的距离.
如图所示，用长为
的绝缘细线悬挂一带电小球，小球质量为m。现加一水平向右、场强为E的匀强电场，平衡时小球静止于A点，细线与竖直方向成θ角。
、
（1）求小球所带电荷量的大小；
（2）若将细线剪断，小球将在时间t内由A点运动到电场中的P点（图中未画出），求A、P两点间的距离；（3）求A、P两点间电势差的
一带电质点从图中的A点竖直向上射入一水平方向的匀强电场中，质点运动到B点时，速度方向变为水平，已知质点质量为m，带电量为q，AB间距离为L，且AB连线与水平方向成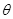
角，求（注意：图中vA、vB未知）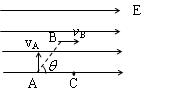
（1）质点从A运动到B时间；
（2）电场强度E；
如图所示，将小砝码置于桌面上的薄纸板上，用水平向右的拉力将纸板迅速抽出，砝码的移动很小，几乎观察不到，这就是大家熟悉的惯性演示实验。若砝码和纸板的质量分别为m1和m2，各接触面间的动摩擦因数均为μ，重力加速度为g。
（1）当纸板相对砝码运动时，求纸板所受摩擦力的大小；
（2）要使纸板相对砝码运动，求所需拉力的大小；
（3）本实验中，m1 =0.5kg，m2 =0.1kg，μ=0.2，砝码与纸板左端的距离d=0.1m，取g ="10" m/ s2。若砝码移动的距离超过l ="0.002" m，人眼就能感知。为确保实验成功，纸板所需的拉力至少多大?