某射手进行射击练习,每射击5发子弹算一组,一旦命中就停止射击,并进入下一组的练习,否则一直打完5发子弹后才能进入下一组练习,若该射手在某组练习中射击命中一次,并且已知他射击一次的命中率为0.8,求在这一组练习中耗用子弹数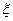 的分布列,并求出
的分布列,并求出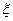 的期望
的期望 与方差
与方差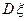 (保留两位小数).
(保留两位小数).
在△ABC中,已知角A、B、C所对的边分别是a、b、c,边c=,且tanA+tanB=tanA·tanB-,又△ABC的面积为S△ABC=,求a+b的值。
如图,甲船在A处,乙船在A处的南偏东45°方向,距A有9n mile并以20n mile/h的速度沿南偏西15°方向航行,若甲船以28n mile/h的速度航行,应沿什么方向,用多少h能尽快追上乙船?
已知双曲线过点(3,-2),且与椭圆 有相同的焦点.
有相同的焦点.
(Ⅰ)求双曲线的标准方程;
(Ⅱ)求以双曲线的右准线为准线的抛物线的标准方程
某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入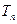 与时间n(以月为单位)的关系为
与时间n(以月为单位)的关系为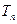 =
= ,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
关于x的不等式 的解集为空集,求实数k的取值范围.
的解集为空集,求实数k的取值范围.