(文科)已知椭圆 过点
过点 和点
和点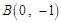 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线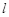 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ,求直线
,求直线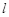 的方程.[来
的方程.[来
设△ABC的内角A、B、C所对的边长分别为a、b、c,且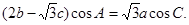
(1)求角A的大小;
(2)若角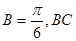 边上的中线AM的长为
边上的中线AM的长为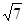 ,求△ABC的面积.
,求△ABC的面积.
已知函数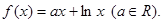
(1)若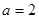 ,求曲线
,求曲线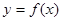 在
在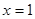 处的切线方程;
处的切线方程;
(2)求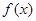 的单调区间;
的单调区间;
(3)设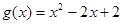 ,若对任意
,若对任意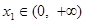 ,均存在
,均存在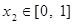 ,使得
,使得 ,求
,求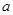 的取值范围.
的取值范围.
已知椭圆 的左右顶点分别为
的左右顶点分别为 ,离心率
,离心率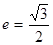 .
.
(1)求椭圆的方程;
(2)若点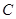 为曲线
为曲线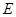 :
: 上任一点(
上任一点(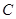 点不同于
点不同于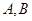 ),直线
),直线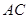 与直线
与直线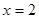 交于点
交于点 ,
,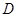 为线段
为线段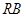 的中点,试判断直线
的中点,试判断直线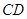 与曲线
与曲线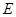 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
已知正项数列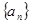 中,
中,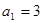 ,前n项和为
,前n项和为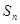
 ,当
,当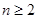 时,有
时,有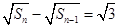 .(1)求数列
.(1)求数列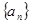 的通项公式;
的通项公式;
(2)记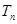 是数列
是数列 的前
的前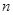 项和,若
项和,若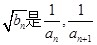 的等比中项,求
的等比中项,求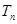 .
.
如图1,在直角梯形 中,
中,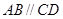 ,
,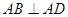 ,且
,且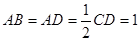 .
.
现以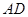 为一边向梯形外作正方形
为一边向梯形外作正方形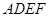 ,然后沿边
,然后沿边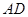 将正方形
将正方形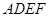 翻折,使平面
翻折,使平面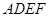 与平面
与平面 垂直,
垂直,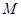 为
为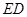 的中点,如图2.
的中点,如图2.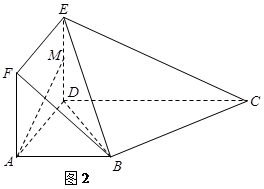
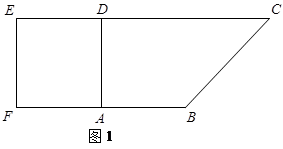
(1)求证: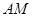 ∥平面
∥平面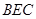 ;
;
(2)求证: ;
;
(3)求点 到平面
到平面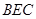 的距离.
的距离.