如图中心在原点,焦点在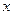 轴上的椭圆,离心率
轴上的椭圆,离心率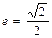 ,且经过抛物线
,且经过抛物线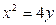 的焦点.
的焦点.
(I)求椭圆的标准方程;
(II)若过点B(2,0)的直线L(斜率不等于零)与椭圆交于不同的两点E、F(E在B、F之间),试求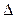 OBE与
OBE与 OBF面积1:2,求直线L的方程。
OBF面积1:2,求直线L的方程。
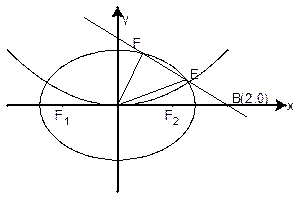 |
已知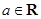 ,函数
,函数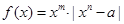 .
.
(1)若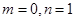 ,写出函数
,写出函数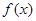 的单调递增区间(不必证明);
的单调递增区间(不必证明);
(2)若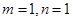 ,当
,当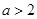 时,求函数
时,求函数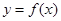 在区间
在区间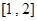 上的最小值.
上的最小值.
经市场调查:生产某产品需投入年固定成本为3万元,每生产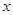 万件,需另投入流动成本为
万件,需另投入流动成本为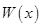 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,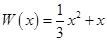 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,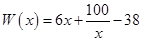 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(1)写出年利润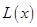 (万元)关于年产量
(万元)关于年产量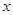 (万件)的函数解析式;
(万件)的函数解析式;
(注:年利润=年销售收入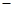 固定成本
固定成本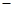 流动成本)
流动成本)
(2)年产量为多少万件时,在这一商品的生产中所获利润最大?最大利润是多少?
已知定义域为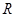 的函数
的函数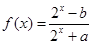 是奇函数.
是奇函数.
(1)求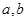 的值;
的值;
(2)利用定义判断函数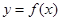 的单调性;
的单调性;
(3)若对任意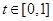 ,不等式
,不等式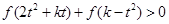 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知复数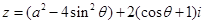 ,其中
,其中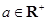 ,
,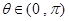 ,
,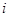 为虚数单位,且
为虚数单位,且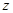 是方程
是方程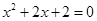 的一个根.
的一个根.
(1)求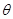 与
与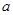 的值;
的值;
(2)若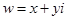 (
(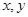 为实数),求满足
为实数),求满足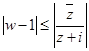 的点
的点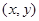 表示的图形的面积.
表示的图形的面积.
设全集是实数集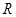 ,
,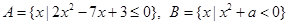 ,
,
(1)当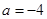 时,求
时,求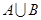 ;
;
(2)若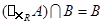 ,求负数
,求负数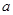 的取值范围.
的取值范围.