经市场调查：生产某产品需投入年固定成本为3万元，每生产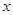
万件，需另投入流动成本为
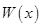万元，在年产量不足8万件时，
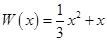（万元），在年产量不小于8万件时，
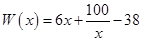（万元）. 通过市场分析，每件产品售价为5元时，生产的商品能当年全部售完.
（1）写出年利润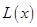
（万元）关于年产量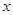（万件）的函数解析式；
（注：年利润=年销售收入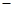
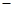固定成本流动成本）
（2）年产量为多少万件时,在这一商品的生产中所获利润最大？最大利润是多少？
已知点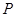
（0，5）及圆
：
．
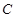（1）若直线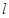
过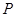且被圆C截得的线段长为4
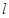，求的方程；
（2）求过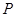点的圆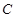的弦的中点的轨迹方程．
如图所示，在四棱锥P－ABCD中，底面ABCD为平行四边形，∠ADC＝45°，AD＝AC＝1，O为AC的中点，PO⊥平面ABCD，PO＝2，M为PD的中点．
（1）证明：PB∥平面ACM；
（2）证明：AD⊥平面PAC．
（1）求与直线
垂直，且与原点的距离为6的直线方程；
（2）求经过直线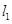
：
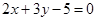与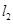
：
的交点，且平行于直线
的直线方程．
某校学生研究性学习小组发现，学生上课的注意力指标随着听课时间的变化而变化，老师讲课开始时，学生的兴趣激增；接下来学生的兴趣将保持较理想的状态一段时间，随后学生的注意力开始分散．设f（t）表示学生注意力指标，该小组发现f（t）随时间t（分钟）的变化规律（f（t）越大，表明学生的注意力越集中）如下：
（a>0，且a≠1）
若上课后第5分钟时的注意力指标为140，回答下列问题：
（Ⅰ）求a的值；
（Ⅱ）上课后第5分钟时和下课前5分钟时比较，哪个时间注意力更集中？
（Ⅲ）在一节课中，学生的注意力指标至少达到140的时间能保持多长？
已知函数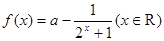
．
（Ⅰ）求证：不论a为何实数f（x）在（﹣∞，+∞）上为增函数；
（Ⅱ）若f（x）为奇函数，求a的值；
（Ⅲ）在（Ⅱ）的条件下，求f（x）在区间[1，5）上的最小值．