已知函数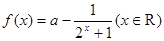 .
.
(Ⅰ)求证:不论a为何实数f(x)在(﹣∞,+∞)上为增函数;
(Ⅱ)若f(x)为奇函数,求a的值;
(Ⅲ)在(Ⅱ)的条件下,求f(x)在区间[1,5)上的最小值.
已知f(x) = ax + ,若 求
求 的范围.
的范围.
已知A、B、C是直线l上的三点,O是直线l外一点,向量 满足
满足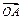 =[f(x)+2f′(1)]
=[f(x)+2f′(1)] -ln(x+1)
-ln(x+1)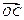
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0,证明:f(x)>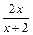 ;
;
(Ⅲ)若不等式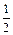 x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
已知数列 中,
中,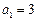 ,
, ,其前
,其前 项和
项和 满足
满足 .令
.令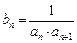 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,求证:
,求证: (
( ).
).
设数列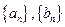 的各项均为正数,若对任意的正整数
的各项均为正数,若对任意的正整数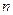 ,都有
,都有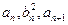 成等差数列,且
成等差数列,且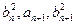 成等比数列.
成等比数列.
(Ⅰ)求证数列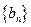 是等差数列;
是等差数列;
(Ⅱ)如果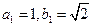 ,求数列
,求数列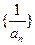 的前
的前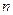 项和。
项和。
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为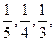 且他们是否破译出密码互不影响.
且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.