（本小题满分14分）某工厂三个车间共有工人1000名，各车间男、女工人数如下表：
| |
第一车间 |
第二车间 |
第三车间 |
| 女工 |
173 |
100 |
 |
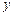| 男工 |
177 |
 |
 |
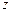已知在全厂工人中随机抽取1名，抽到第二车间男工的概率是0.15.
(1)求的值；
(2)现用分层抽样的方法在全厂抽取50名工人，问应在第三车间抽取多少名？
(3)已知
,求第三车间中女工比男工少的概率.
已知函数f（x）=
, 其中为常数，若当x∈（－∞, 1］时, f（x）有意义，求实数a的取值范围．
在数列{an}中，a1＝15，以后各项由 an+1＝an－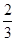
，求数列{an}的前n项和的最大值．
已知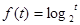
，t∈[
，8]，对于f（t）值域内的所有实数m，不等式
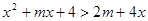恒成立，求x的取值范围。
已知函数f（x）=
（a＞0,x＞0）.
（1）求证:f（x）在（0,+∞）上是增函数；
（2）若f（x）≤2x在（0,+∞）上恒成立，求a的取值范围；
（3）若f（x）在［m,n］上的值域是［m,n］（m≠n），求a的取值范围.
已知函数f（x）=6x–6x2，设函数g1（x）=f（x）, g2（x）=f［g1（x）］, g3（x）="f" ［g2（x）］,…gn（x）=f［gn–1（x）］,…
（1）求证：如果存在一个实数x0，满足g1（x0）=x0，那么对一切n∈N，gn（x0）=x0都成立；
（2）若实数x0满足gn（x0）=x0，则称x0为稳定不动点，试求出所有这些稳定不动点；
（3）设区间A=（–∞,0）,对于任意x∈A，有g1（x）=f（x）=a＜0, g2（x）=f［g1（x）］=f（0）＜0，且n≥2时，gn（x）＜0.试问是否存在区间B（A∩B≠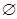
），对于区间内任意实数x，只要n≥2，都有gn（x）＜0.