(本小题满分12分)
已知函数 的定义域为R, 对任意实数
的定义域为R, 对任意实数 都有
都有 ,
,
且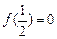 , 当
, 当 时,
时,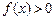 .
.
(1) 求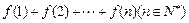 ;
;
(2) 判断函数 的单调性并证明.
的单调性并证明.
如果项数均为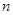
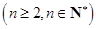 的两个数列
的两个数列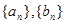 满足
满足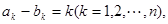 且集合
且集合 ,则称数列
,则称数列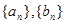 是一对“
是一对“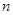 项相关数列”.
项相关数列”.
(Ⅰ)设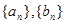 是一对“4项相关数列”,求
是一对“4项相关数列”,求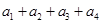 和
和 的值,并写出一对“
的值,并写出一对“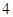 项
项
关数列”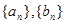 ;
;
(Ⅱ)是否存在“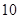 项相关数列”
项相关数列”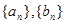 ?若存在,试写出一对
?若存在,试写出一对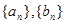 ;若不存在,请说明理由;
;若不存在,请说明理由;
(Ⅲ)对于确定的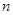 ,若存在“
,若存在“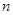 项相关数列”,试证明符合条件的“
项相关数列”,试证明符合条件的“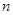 项相关数列”有偶数对.
项相关数列”有偶数对.
已知函数 ,
, .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)设点 为函数
为函数 的图象上任意一点,若曲线
的图象上任意一点,若曲线 在点
在点 处的切线的斜率恒大于
处的切线的斜率恒大于 ,
,
求 的取值范围.
的取值范围.
已知函数 ,
, .
.
(Ⅰ)若函数 在
在 上至少有一个零点,求
上至少有一个零点,求 的取值范围;
的取值范围;
(Ⅱ)若函数 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
已知数列 ,
, 的通项
的通项 ,
, 满足关系
满足关系 ,且数列
,且数列 的前
的前 项和
项和
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
在△ 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,
, .
.
(Ⅰ)求△ 的面积;
的面积;
(Ⅱ)若 ,求
,求 的值.
的值.