现有流量均为300
的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2
和0.2.假设从汇合处开始,沿岸设有若干个观测点,两股水流在流经相邻两个观测点的过程中,其混合效果相当于两股水流在1秒钟内交换100
的水量,即从A股流入B股100水,经混合后,又从B股流入A股100水并混合.问：从第几个观测点开始,两股河水的含沙量之差小于0.01（不考虑泥沙沉淀）？
（本小题满分12分）已知全集U = R，非空集合
，
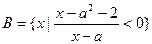.（Ⅰ）当
时，求（∁U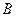
)
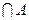；（Ⅱ）命题
，命题
，若
是
的必要条件，求实数
的取值范围.
设函数
．
（1）若
时函数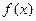
有三个互不相同的零点，求
的取值范围；
（2）若函数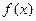在
内没有极值点，求
的取值范围；
（3）若对任意的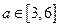
，不等式
在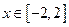
上恒成立，求实数的取值范围．
经过长期观测得到：在交通繁忙的时段内某公路汽车的车流量y（千辆／时）与汽车的平均速度v（千米／时）之间的函数关系为
（1）在该时段内，当汽车的平均
速度v为多少时，车流量最大？最大车流量是多少（精确到0.1千辆／时）？
（2）若要求在该时段内车流量超过10千辆／时，则汽车的平均速度应该在什么范围内？
设
、b是满足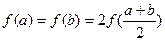
的实数，其中
.
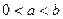（1）求证：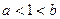
；（2）求证：
.
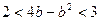已知
，且
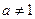，求证：