设 ,
,
(1)令 ,讨论
,讨论 在(0.+∞)内的单调性并求极值;
在(0.+∞)内的单调性并求极值;
(2)求证:当 时,恒有
时,恒有 。
。
(本小题满分14分)已知两圆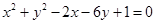 和
和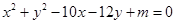
(1)m取何值时,两圆外切;
(2)m取何值时,两圆内切;
(3)求m=45时两圆的公共弦所在直线的方程和公共弦的长.
已知圆C经过A(3,2),B(1,6)圆心在直线y=2x上。
(1)求圆C方程;(2)若直线 x+2y+m=0与圆C相交于M、N两点,且∠MAN=600,求m的值。
已知直线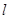 经过直线
经过直线 与直线
与直线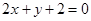 的交点
的交点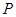 ,且垂直于直线
,且垂直于直线 .
.
(1)求直线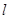 的方程;
的方程;
(2)求直线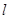 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积 .
.
(本小题10分)如图,在三棱锥P-ABC中, 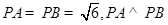 ,
, ,平面PAB
,平面PAB  平面ABC.
平面ABC.
(1)求证:PA  BC:
BC:
(2)求PC的长度;
(3)求二面角P-AC-B的正切值
(本小题8分)已知点P(-4,0)及圆C:
(1)当直线  过点P且与圆心C的距离为l时,求直线
过点P且与圆心C的距离为l时,求直线  的方程:
的方程:
(2)设过点P的直线与圆C交于A、B两点,当  取得最小值时,求以线段AB为直径的圆的方程,
取得最小值时,求以线段AB为直径的圆的方程,