(文科)已知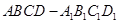 是底面边长为1的正四棱柱,高
是底面边长为1的正四棱柱,高 .求:
.求:
⑵ 异面直线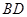 与
与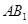 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示);
⑵ 四面体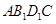 的体积.
的体积.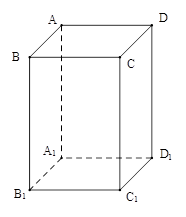
已知p: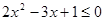 ,q:
,q: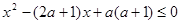
(1)若a=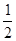 ,且
,且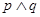 为真,求实数x的取值范围.
为真,求实数x的取值范围.
(2)若p是q的充分不必要条件,求实数a的取值范围.
在△ABC中,角A,B,C所对的边分别是a,b,c.已知(b-2a)cosC+c cosB=0.
(1)求C;
(2)若c=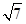 ,b=3a,求△ABC的面积.
,b=3a,求△ABC的面积.
已知数列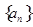 的前
的前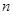 项和为
项和为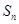 ,且
,且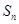 =
=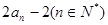 ,数列
,数列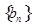 中,
中,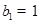 , 点
, 点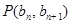 (
(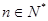 )在直线
)在直线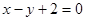 上.
上.
(1)求数列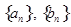 的通项
的通项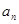 和
和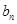 ;
;
(2)设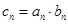 ,求数列
,求数列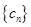 的前n项和
的前n项和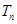 ,并求满足
,并求满足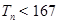 的最大正整数
的最大正整数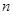 .
.
如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),.道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.
设△ABC的内角A,B,C所对边的长分别是a,b,c,且b=4,c=2,A=2B.
(1)求a的值;(2)求sin 的值.
的值.