甲、乙两位同学做摸球游戏,游戏规则规定:两人轮流从一个放有2个红球,3个黄球,1个白球且颜色不同的6个小球的暗箱中取球,每次每人只能取一球,每取出1个后立即放回,另一个接着再取出后也立即放回,谁先取到红球,谁为胜者.现甲先取,求甲摸求次数不超过3次就获胜的概率.
已知椭圆 :
: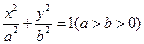 的离心率为
的离心率为 ,且过点
,且过点 ,设椭圆的右准线
,设椭圆的右准线 与
与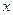 轴的交点为
轴的交点为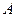 ,椭圆的上顶点为
,椭圆的上顶点为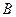 ,直线
,直线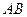 被以原点为圆心的圆
被以原点为圆心的圆 所截得的弦长为
所截得的弦长为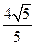 .
.
⑴求椭圆 的方程及圆
的方程及圆 的方程;
的方程;
⑵若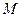 是准线
是准线 上纵坐标为
上纵坐标为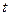 的点,求证:存在一个异于
的点,求证:存在一个异于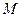 的点
的点 ,对于圆
,对于圆 上任意一点
上任意一点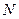 ,有
,有 为定值;且当
为定值;且当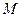 在直线
在直线 上运动时,点
上运动时,点 在一个定圆上.
在一个定圆上.
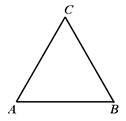
如图,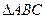 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰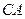 的长为
的长为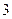 (百米),底
(百米),底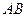 的长为
的长为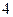 (百米).现决定在空地内筑一条笔直的小路
(百米).现决定在空地内筑一条笔直的小路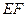 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为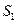 和
和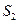 .
.
⑴若小路一端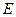 为
为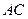 的中点,求此时小路的长度;
的中点,求此时小路的长度;
⑵求 的最小值.
的最小值.
在菱形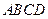 中,
中, ,线段
,线段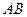 的中点是
的中点是 ,现将
,现将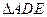 沿
沿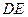 折起到
折起到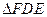 的位置,使平面
的位置,使平面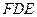 和平面
和平面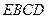 垂直,线段
垂直,线段 的中点是
的中点是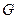 .
.
⑴证明:直线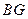 ∥平面
∥平面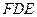 ;
;
⑵判断平面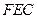 和平面
和平面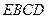 是否垂直,并证明你的结论.
是否垂直,并证明你的结论.
(本小题满分14分)
已知函数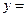
 的定义域为R, 且对于任意
的定义域为R, 且对于任意 R,存在正实数
R,存在正实数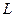 ,使得
,使得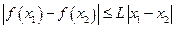 都成立.
都成立.
若 ,求
,求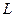 的取值范围;
的取值范围;
当 时,数列
时,数列 满足
满足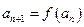 ,
, .
.
证明: ;
;
令 ,证明:
,证明: .
.
(本小题满分14分)
已知函数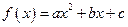
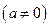 满足
满足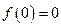 ,对于任意
,对于任意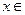 R都有
R都有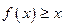 ,且
,且 ,令
,令 .
.
(1)求函数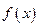 的表达式;
的表达式;
(2)求函数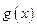 的单调区间;
的单调区间;
研究函数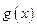 在区间
在区间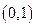 上的零点个数.
上的零点个数.