已知数列 的前
的前 项和为
项和为 ,对任意
,对任意 ,点
,点 都在函数
都在函数 的图像上.
的图像上.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,且数列
,且数列 是等差数列,求非零常数
是等差数列,求非零常数 的值;
的值;
在平面直角坐标系中,O为坐标原点,已知点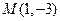 ,
, ,
,
若点C满足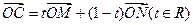 ,点C的轨迹与抛物线
,点C的轨迹与抛物线 交于A、B两点.
交于A、B两点.
(I)求证: ;
;
(II)在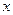 轴正半轴上是否存在一定点
轴正半轴上是否存在一定点 ,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
已知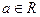 ,
,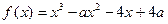 .
.
(I)若 ,求函数
,求函数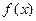 在区间
在区间 的最大值与最小值;
的最大值与最小值;
(II)若函数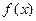 在区间
在区间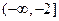 和
和 上都是增函数,求实数
上都是增函数,求实数 的取值范围.
的取值范围.
某家具城进行促销活动,促销方案是:顾客每消费1000元,便可以获得奖券一张,每张奖券中奖的概率为 ,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券.
,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券.
(I)求家具城恰好返还该顾客现金200元的概率;
(II)(文科)求家具城至少返还该顾客现金200元的概率.
(理科)设该顾客有 张奖券中奖,求
张奖券中奖,求 的分布列,并求
的分布列,并求 的数学
的数学
期望E.
在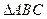 中,a、b、c分别为角A、B、C的对边,且满足
中,a、b、c分别为角A、B、C的对边,且满足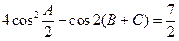
(I)求角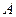 大小;
大小;
(II)若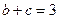 ,当
,当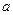 取最小值时,求
取最小值时,求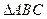 的面积.
的面积.
如图,四棱锥
中,底面
为矩形,
,
,
,
在侧棱
上,
.
(I)证明:
是侧棱
的中点;
(Ⅱ)求二面角
的大小.