已知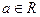 ,
,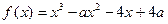 .
.
(I)若 ,求函数
,求函数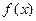 在区间
在区间 的最大值与最小值;
的最大值与最小值;
(II)若函数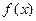 在区间
在区间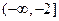 和
和 上都是增函数,求实数
上都是增函数,求实数 的取值范围.
的取值范围.
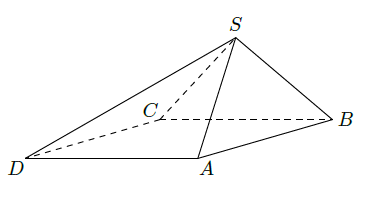
四棱锥 中,底面 为平行四边形,侧面 底面 ,已知 .
(Ⅰ)证明
;
(Ⅱ)求直线
与平面
所成角的大小.
某商场经销某商品,根据以往资料统计,顾客采用的付款期数
的分布列为
| 1 | 2 | 3 | 4 | 5 | |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.
表示经销一件该商品的利润.
(Ⅰ)求事件
"购买该商品的3位顾客中,至少有1位采用1期付款"的概率
;
(Ⅱ)求
的分布列及期望
.
设锐角三角形
的内角
的对边分别为
.
(Ⅰ)求
的大小;
(Ⅱ)求
的取值范围.
设函数
.
(Ⅰ)解不等式
;
(Ⅱ)求函数
的最小值.
和
的极坐标方程分别为
.
(Ⅰ)把
和
的极坐标方程化为直角坐标方程;
(Ⅱ)求经过
交点的直线的直角坐标方程.