设锐角三角形
的内角
的对边分别为
.
(Ⅰ)求
的大小;
(Ⅱ)求
的取值范围.
设 是函数
是函数 的一个极值点.
的一个极值点.
(1)求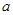 与
与 的关系式(用
的关系式(用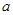 表示
表示 );
);
(2)求 的单调区间;
的单调区间;
(3)设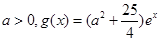 ,若存在
,若存在 ,使得
,使得 成立,求实数
成立,求实数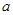 的取值范围.
的取值范围.
设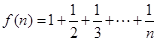 ,是否存在
,是否存在 使等式:
使等式: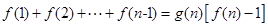 对任意
对任意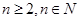 都成立,并证明你的结论.
都成立,并证明你的结论.
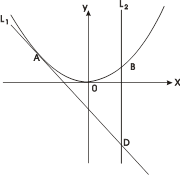
已知 为曲线
为曲线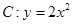 上的点,直线
上的点,直线 过点
过点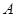 ,且与曲线
,且与曲线 相切,直线
相切,直线 交曲线
交曲线 于
于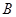 ,交直线
,交直线 于点
于点 .
.
(1) 求直线 的方程;
的方程;
(2)设 的面积为
的面积为 ,求
,求 的值;
的值;
(3)设由曲线 ,直线
,直线 ,
, 所围成的图形的面积为
所围成的图形的面积为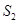 ,求证
,求证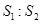 的值为与
的值为与 无关的常数.
无关的常数.
已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品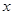 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为 万元,且
万元,且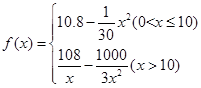
(1)写出年利润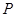 (万元)关于年产品
(万元)关于年产品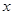 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该企业生产此产品所获年利润最大?
(注:年利润=年销售收入-年总成本)
在二项式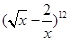 的展开式中
的展开式中
(1)求展开式中含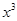 项的系数;
项的系数;
(2)如果第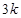 项和第
项和第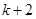 项的二项式系数相等,试求
项的二项式系数相等,试求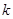 的值.
的值.