(本小题满分12分)
用黄、蓝、白三种颜色粉刷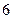 间办公室
间办公室
(Ⅰ) 若每间办公室刷什么颜色不要求,有多少种不同的粉刷方法?
(Ⅱ)若一种颜色粉刷 间,一种颜色粉刷
间,一种颜色粉刷 间,一种颜色粉刷
间,一种颜色粉刷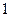 间,有多少种不同的粉刷方法?
间,有多少种不同的粉刷方法?
(Ⅲ)若每种颜色至少用一次,粉刷这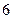 间办公室,有多少种不同的粉刷方法?
间办公室,有多少种不同的粉刷方法?
解:
(满分12分)如图,在直三棱柱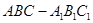 中,∠ACB=90°;AC=BC=CC1=2。
中,∠ACB=90°;AC=BC=CC1=2。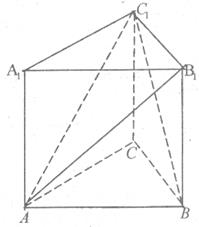
(1)求证:AB1⊥BC1;
(2)求点B到平面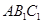 的距离;
的距离;
(3)求二面角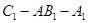 的大小。
的大小。
(满分12分)在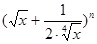 的展开式中,前三项的系数成等差数列。
的展开式中,前三项的系数成等差数列。
(Ⅰ)求展开式中含有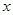 的项的系数;
的项的系数;
(Ⅱ)求展开式中的有理项。
(满分10分)在曲线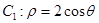 上求一点,使它到直线
上求一点,使它到直线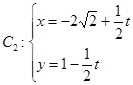 (
(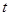 为参数)的距离最小,并求出该点坐标和最小距离。
为参数)的距离最小,并求出该点坐标和最小距离。
选修4-5:不等式选讲
已知函数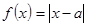
(1)若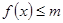 的解集为
的解集为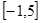 ,求实数
,求实数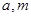 的值;
的值;
(2)当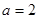 且
且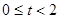 时,解关于
时,解关于 的不等式
的不等式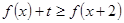
选修4-4:坐标系与参数方程选讲
在直角坐标系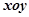 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以原点为极点,以
为参数),以原点为极点,以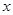 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线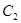 的极坐标方程为
的极坐标方程为
(1)求曲线 的普通方程与曲线
的普通方程与曲线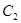 的直角坐标方程;
的直角坐标方程;
(2)设点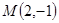 ,曲线
,曲线 与曲线
与曲线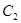 交于
交于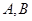 ,求
,求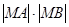 的值.
的值.