模块3-5试题
(I) 首先提示了原子具有复杂的结构, 首先揭示了原子核具有复杂的结构。
| A.电子的发现 | B.质子的发现 |
| C.中子的发现 | D.天然放射现象的发现 |
(II)介子由两个夸克构成,而夸克之间的相互作用相当复杂。研究介子可通过用高能电子与其发生弹性碰撞来进行。由于碰撞过程难于分析,为掌握其主要内涵,人们假设了一种简化了的“分粒子”模型。其主要内容为:电子只和介子的某部分(比如其中一个夸克)做弹性碰撞。碰撞后的夸克再经过介子内的相互作用把能量和动量传给整个介子。“分粒子”模型可用下面的简化模型来阐述:一个电子质量为m1,动能为E0,与介子的一个夸克(质量为m2)做弹性碰撞。介子里另一个夸克的质量为m3,夸克间以一根无质量的弹簧相连。碰撞前夸克处于静止状态,弹簧处于自然长度。试求:
(1)夸克m2与电子碰撞后所获得的动能
(2)介子作为一个整体所具有的以弹簧弹性势能形式代表的介子的最大内能。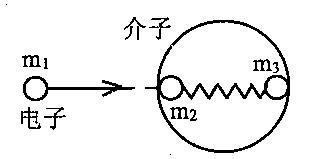
甲、乙两辆汽车沿平直公路同向匀速行驶,甲车在乙车前面,它们之间相距x0=40m,速度均为v0=10m/s.某时刻,甲车刹车作匀减速直线运动,加速度大小为5m/s2.从此时刻起,求:
(1)甲车经过多长时间停止运动?
(2)当甲车静止时,甲、乙两辆汽车之间的距离为多大?
(3)经多长时间两车相遇?
如图所示,在y>0的空间中存在匀强电场,场强沿y轴负方向;在y<0的空间中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外.一电荷量为q、质量为m的带正电的运动粒子,经过y轴上y=h处的点P1时速率为v0,方向沿x轴正方向;然后经过x轴上x=2h处的P2点进入磁场,并经过y轴上y=-2h处的P3点.不计重力,求:
(1)电场强度的大小;
(2)粒子到达P2时速度的大小和方向;
(3)磁感应强度的大小.
如图所示,匀强磁场宽L="30" cm,B=3.34×10-3 T,方向垂直纸面向里.设一质子以v=1.6×105 m/s 的速度垂直于磁场B的方向从小孔C射入磁场,然后打到照相底片上的A点.试求:
(1)质子在磁场中运动的轨道半径r;
(2)A点距入射线方向上的O点的距离H;
(3)质子从C孔射入到A点所需的时间t.(质子的质量为1.67×10-27 kg;质子的电荷量为1.6×10-19 C)
(10分)如图,金属杆ab的质量为m,长为L,通过的电流为I,处在磁感应强度为B的匀强磁场中,结果金属杆ab静止且紧压在水平导轨上.若磁场方向与导轨平面成θ角,求:
(1)金属杆ab受到的摩擦力大小;
(2)金属杆ab对导轨的压力大小.
如图所示,在倾角为α的光滑斜面上,水平放置一长为L、质量为m的直导线,通以从A到B的电流I.现在要加一个垂直于AB的匀强磁场,使AB能保持静止.那么所加磁场的磁感应强度B的大小和方向如何?