(本小题满分12分)
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(I)求出该几何体的体积;
(II)求证:EM∥平面ABC;
|
(III)试问在棱DC上是否存在点N,使NM⊥平面 ?若存在,确定点N的位置;
?若存在,确定点N的位置; 若不存在,请说明理由.
若不存在,请说明理由.
已知椭圆: (
( )上任意一点到两焦点距离之和为
)上任意一点到两焦点距离之和为 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,点
,点 是右准线上任意一点,过
是右准线上任意一点,过 作直线
作直线 的垂线
的垂线 交椭圆于
交椭圆于 点.
点.
(1)求椭圆 的标准方程;
的标准方程;
(2)证明:直线 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;
(3)点 的纵坐标为3,过
的纵坐标为3,过 作动直线
作动直线 与椭圆交于两个不同点
与椭圆交于两个不同点 ,在线段
,在线段 上取点
上取点 ,满足
,满足 ,试证明点
,试证明点 恒在一定直线上.
恒在一定直线上.
设函数 ,
, .
.
(1)记 为
为 的导函数,若不等式
的导函数,若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(2)若 ,对任意的
,对任意的 ,不等式
,不等式 恒成立.求
恒成立.求 (
( ,
, )的值.
)的值.
已知在直角坐标系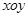 中,曲线
中,曲线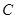 的参数方程为
的参数方程为 (
(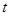 为非零常数,
为非零常数,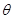 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系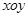 取相同的长度单位,且以原点
取相同的长度单位,且以原点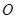 为极点,以
为极点,以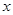 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的方程为
的方程为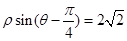 .
.
(Ⅰ)求曲线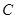 的普通方程并说明曲线的形状;
的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数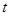 ,使得直线
,使得直线 与曲线
与曲线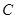 有两个不同的公共点
有两个不同的公共点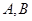 ,且
,且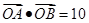 (其中
(其中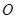 为坐标原点)?若存在,请求出;否则,请说明理由.
为坐标原点)?若存在,请求出;否则,请说明理由.
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在 ,(单位:元).
,(单位:元).
(Ⅰ)估计居民月收入在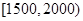 的概率;
的概率;
(Ⅱ)根据频率分布直方图估计样本数据的中位数;
(Ⅲ)若将频率视为概率,从本地随机抽取3位居民(看做有放回的抽样),求月收入在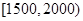 的居民数X的分布列和数学期望.
的居民数X的分布列和数学期望.
已知函数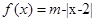 ,
,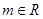 ,且
,且 的解集为
的解集为 .
.
(1)求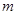 的值;
的值;
(2)若 ,且
,且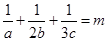 ,求
,求 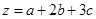 的最小值.
的最小值.