(本小题满分12分)
已知曲线 上任意一点
上任意一点 到点
到点 的距离比它到直线
的距离比它到直线 的距离小1.
的距离小1.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)直线 与曲线
与曲线 相交于
相交于 两点,
两点, 设直线
设直线 的斜率分别为
的斜率分别为
求证: 为定值.
为定值.
已知多面体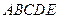 中,
中, 平面
平面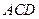 ,
, 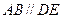 ,
,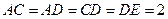 ,
,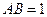 ,
,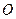 为
为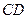 的中点
的中点
(Ⅰ)求证: 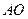
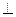 平面
平面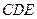 .
.
(Ⅱ)求直线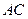 与平面
与平面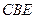 所成角的大小.
所成角的大小.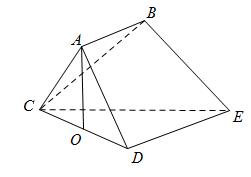
甲盒有标号分别为1、2、3的3个红球;乙盒有标号分别为1、2、…、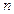
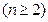
的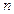 个黑球,从甲、乙两盒中各抽取一个小球,抽到标号为1号红球和
个黑球,从甲、乙两盒中各抽取一个小球,抽到标号为1号红球和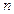 号黑球的概率为
号黑球的概率为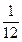 .
.
(Ⅰ)求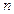 的值;
的值;
(Ⅱ)现从甲乙两盒各随机抽取1个小球,抽得红球的得分为其标号数;抽得黑球,若标号数为奇数,则得分为1,若标号数为偶数,则得分为0.求得分为2的概率.
在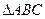 中,角
中,角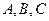 所对的边分别为
所对的边分别为 .向量
.向量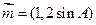 ,
,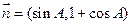 .已知
.已知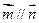 ,
, .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)判断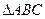 的形状并证明.
的形状并证明.
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知定圆 ,动圆
,动圆 过点
过点 且与圆
且与圆 相切,记动圆圆
相切,记动圆圆
心 的轨迹为
的轨迹为 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)若点 为曲线
为曲线 上任意一点,证明直线
上任意一点,证明直线 与曲线
与曲线 恒有且只有一个公共点.
恒有且只有一个公共点.
(Ⅲ)由(Ⅱ)你能否得到一个更一般的结论?并且对双曲线 写出一个类似的结论(皆不必证明).
写出一个类似的结论(皆不必证明).