(本小题共13分)
口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5.甲先摸出一个球,记下编号为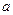 ,放回袋中后,乙再摸一个球,记下编号为
,放回袋中后,乙再摸一个球,记下编号为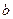 .
.
(Ⅰ)求“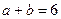 ”的事件发生的概率;
”的事件发生的概率;
(Ⅱ)若点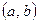 落在圆
落在圆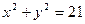 内,则甲赢,否则算乙赢,这个游戏规则公平吗?试说明理由.
内,则甲赢,否则算乙赢,这个游戏规则公平吗?试说明理由.
(本小题满分14分)
对于函数 ,若存在
,若存在 ,使
,使 成立,则称
成立,则称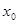 为
为 的一个不动点.设函数
的一个不动点.设函数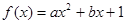 (
( ).
).
(Ⅰ)当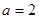 ,
, 时,求
时,求 的不动点;
的不动点;
(Ⅱ)若 有两个相异的不动点
有两个相异的不动点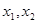 .
.
(i)当 时,设
时,设 的对称轴为直线
的对称轴为直线 ,求证:
,求证: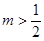 ;
;
(ii)若 ,且
,且 ,求实数
,求实数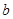 的取值范围.
的取值范围.
(本小题满分15分)
设数列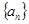 满足
满足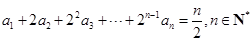 .
.
(Ⅰ)求 ;
;
(Ⅱ)设 ,
, ,求证:数列
,求证:数列 中
中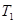 最小.
最小.
(本小题满分15分)
已知椭圆 :
: (
(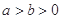 )的一个焦点为
)的一个焦点为 ,且
,且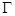 上一点到其两焦点的距离之和为
上一点到其两焦点的距离之和为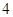 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线 与椭圆
与椭圆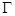 交于不同两点
交于不同两点 ,若点
,若点 满足
满足 ,求实数
,求实数 的值.
的值.
(本小题满分15分)
已知抛物线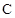 :
: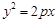
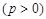 的焦点为
的焦点为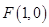 ,过
,过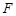 且斜率为
且斜率为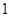 的直线
的直线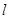 交抛物线
交抛物线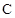 于
于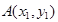 ,
,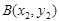 两点.
两点.
(Ⅰ)求抛物线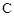 的标准方程;
的标准方程;
(Ⅱ)求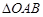 的面积.
的面积.
等差数列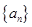 中,
中,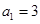 ,
, .
.
(Ⅰ)求数列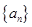 的通项公式;
的通项公式;
(Ⅱ)设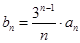 ,求数列
,求数列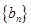 的前
的前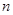 项和
项和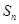 .
.