(本小题满分12分)已知三棱锥P—ABC中,PC⊥底面ABC,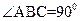 ,
, ,
,
二面角P-AB-C为 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.
(Ⅰ)求证:AP⊥平面BDE;
(Ⅱ)求直线EB与平面PAC所成的角。
设函数f(x)=cos(2x﹣ )+2cos2x,
)+2cos2x,
(Ⅰ)求f(x)的最大值,并写出使f(x)取最大值时x的集合;
(Ⅱ)已知△ABC中,角A、B、C的对边分别为a、b、c,若f(B+C)= ,b+c=2,a=1,求△ABC的面积的最大值.
,b+c=2,a=1,求△ABC的面积的最大值.
【选修4-5:不等式选讲】
(1)设函数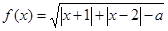 的定义域为
的定义域为 ,试求
,试求 的取值范围;
的取值范围;
(2)已知实数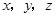 满足
满足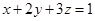 ,求
,求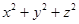 的最小值.
的最小值.
【选修4-4:坐标系与参数方程】
已知曲线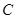 的参数方程为:
的参数方程为: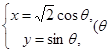 为参数),直线
为参数),直线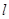 的参数方程为:
的参数方程为: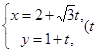 为参数),点
为参数),点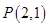 ,直线
,直线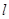 与曲线
与曲线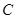 交于
交于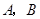 两点.
两点.
(1)写出曲线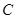 和直线
和直线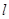 在直角坐标系下的标准方程;
在直角坐标系下的标准方程;
(2)求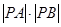 的值.
的值.
【选修4-1:几何证明选讲】
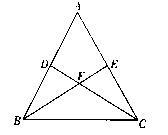
如图,在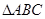 中,
中,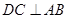 于
于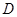 ,
,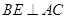 于
于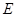 ,
,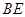 交
交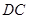 于点
于点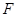 ,若
,若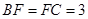 ,
,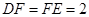 .
.
(1)求证: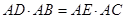 ;
;
(2)求线段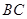 的长度.
的长度.
已知函数 .
.
(1)若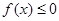 恒成立,试确定实数
恒成立,试确定实数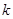 的取值范围;
的取值范围;
(2)证明: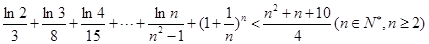 .
.