设 ,
, 是给定的两个正整数.证明:有无穷多个正整数
是给定的两个正整数.证明:有无穷多个正整数 ,使得
,使得 与
与 互素.
互素.
(本小题满分16分)如图,有一个长方形地块ABCD,边AB为2km, AD为4 km.,地块的一角是湿地(图中阴影部分),其边缘线AC是以直线AD为对称轴,以A为顶点的抛物线的一部分.现要铺设一条过边缘线AC上一点P的直线型隔离带EF,E,F分别在边AB,BC上(隔离带不能穿越湿地,且占地面积忽略不计).设点P到边AD的距离为t(单位:km),△BEF的面积为S(单位:  ).
).
(1)求S关于t的函数解析式,并指出该函数的定义域;
(2)是否存在点P,使隔离出的△BEF面积S超过3  ?并说明理由.
?并说明理由.
(本小题满分14分)在平面直角坐标系xOy中,己知点  ,C, D分别为线段OA, OB上的动点,且满足AC=BD.
,C, D分别为线段OA, OB上的动点,且满足AC=BD.
(1)若AC=4,求直线CD的方程;
(2)证明: OCD的外接圆恒过定点(异于原点O).
OCD的外接圆恒过定点(异于原点O).
(本小题满分14分)如图,在三棱锥P- ABC中,已知平面PBC  平面ABC.
平面ABC.
(1)若AB BC,CP
BC,CP PB,求证:CP
PB,求证:CP PA:
PA:
(2)若过点A作直线 ⊥平面ABC,求证:
⊥平面ABC,求证: //平面PBC.
//平面PBC.
(本小题满分14分)己知向量 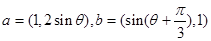 ,
, 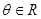 .
.
(1)若 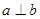 ,求
,求 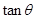 的值:
的值:
(2)若 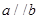 ,且
,且 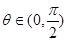 ,求
,求 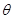 的值.
的值.
若实数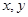 满足
满足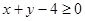 ,则
,则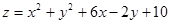 的最小值为_______.
的最小值为_______.