【选修4—5:不等式选讲】 设函数
 >1),且
>1),且 的最小值为
的最小值为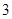 ,若
,若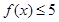 ,求
,求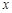 的取值范围。
的取值范围。
如图,
是圆
的直径,点
是圆
上异于
的点,直线
平面
,
分别是
的中点.
(1)记平面
与平面
的交线为
,试判断直线l与平面
的位置关系,并加以证明;
(2)设(1)中的直线
与圆
的另一个交点为
,且点
满足
.记直线
与平面
所成的角为
,异面直线与
所成的角为
,二面角
的大小为
.求证:
.
已知等比数列
满足:
.
(1)求数列
的通项公式;
(2)是否存在正整数
,使得
?若存在,求
的最小值;若不存在,说明理由.
在
中,角
对应的边分别是
,已知
.
(1)求角
的大小;
(2)若
的面积
,求
的值.
设 ,集合
(1)求集合
(用区间表示)
(2)求函数
在
内的极值点.
在平面直角坐标系
中,已知椭圆
的左焦点为
,且点
在
上。
(1)求椭圆
的方程;
(2)设直线
同时与椭圆
和抛物线
相切,求直线
的方程.