. (满分12分)
矩形ABCD的对角线AC、BD相交于点M (2,0),AB边所在直线的方程为: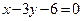
.
若点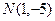
在直线AD上.
（1）求点A的坐标及矩形ABCD外接圆的方程；
（2）过直线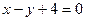
上一点P作（1）中所求圆的切线，设切点为E、F，求四边形PEMF面积的最小值，并求此时
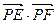的值.
(满分12分)
已知函数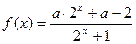
是定义在R上的奇函数.
（1）求
的值；
（2）判断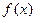
在R上的单调性并用定义证明；
（3）若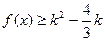
对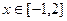
恒成立,求实数k的取值范围.
(满分12分)已知圆C的方程为：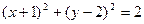
（1）若圆C的切线l在x轴和y轴上的截距相等，求切线l的方程；
（2）过原点的直线m与圆C相交于A、B两点，若|AB|=2，求直线m的方程.
(本题满分12分)
已知等差数列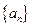
的首项为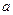
，公差为b，且不等式
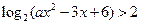的解集为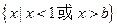
．
（1）求数列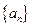的通项公式及前n项和
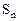公式 ；
（2）求数列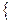
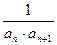
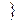的前n项和Tn .
(满分12分)
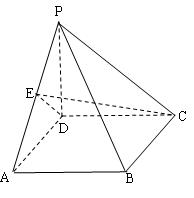
如图，四棱锥P-ABCD中，PD⊥底面ABCD,底面ABCD是矩形.
（1）若PD=AD,E为PA的中点，求证：平面CDE⊥平面PAB;
（2）F是棱PC上的一点，CF=CP，问线段AC上是否存在一点M，使得PA∥平面DFM.若存在，指出点M在AC边上的位置，并加以证明；若不存在，说明理由.19. (满分12分)