某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
| 品种甲 |
403 |
397 |
390 |
404 |
388 |
400 |
412 |
406 |
| 品种乙 |
419 |
403 |
412 |
418 |
408 |
423 |
400 |
413 |
(1)假设n=2,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如表:分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
(本小题满分12分)已知圆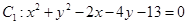 与圆
与圆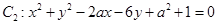 (其中
(其中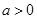 ) 相外切,且直线
) 相外切,且直线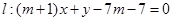 与圆
与圆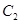 相切,求
相切,求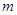 的值.
的值.
(本小题满分12分)已知圆C: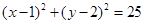 ,直线L:
,直线L: 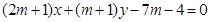
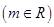
(1) 证明:无论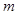 取什么实数,L与圆恒交于两点;
取什么实数,L与圆恒交于两点;
(2) 求直线被圆C截得的弦长最小时直线L的斜截式方程.
(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.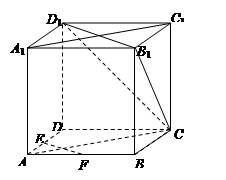
(1)求证:EF ∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
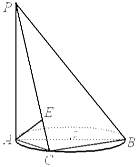
(本小题满分12分)如图,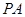 垂直于⊙
垂直于⊙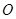 所在的平面,
所在的平面,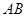 是⊙
是⊙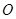 的直径,
的直径,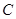 是⊙
是⊙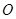 上一点,过点
上一点,过点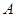 作
作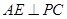 ,垂足为
,垂足为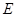 .
.
求证: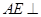 平面
平面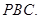
(本小题满分10分)过点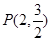 的直线
的直线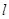 与
与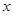 轴的正半轴、
轴的正半轴、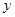 轴的正半轴分别交于点
轴的正半轴分别交于点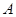 、
、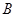 ,
,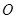 为坐标原点,
为坐标原点,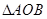 的面积等于6,求直线
的面积等于6,求直线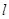 的方程.
的方程.