现需要设计一个仓库，它由上下两部分组成,上部分的形状是正四棱雉 ,下部分的形状是正四棱柱 (如图所示)，并要求正四棱柱的高 的四倍.
(1)若 ,则仓库的容积是多少?
(2)若正四棱柱的侧棱长为 ，则当 为多少时,仓库的容积最大？
某校高一某班的一次数学测试成绩（满分100分）的茎叶图和频率分布直方图都受到不同程度的污染，但可见部分如下，据此解答如下问题：
(Ⅰ) 求分数在[50,60)的频率及全班人数；
(Ⅱ) 求分数在[80,90)之间的频数，并计算频率分布直方图中[80,90)间的矩形的高；
（Ⅲ）若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[90,100]之间的概率.
2005年10月12日，我国成功发射了“神州”六号载人飞船，这标志着中国人民又迈出了具有历史意义的一步。已知火箭的起飞重量M是箭体（包括搭载的飞行器）的重量m和燃料重量x之和。在不考虑空气阻力的条件下，假设火箭的最大速度y关于x的函数关系式为：
当燃料重量为
吨（e为
自然对数的底数，
）时，该火箭的最大速度为4（km/s）.
（1）求火箭的最大速度
与燃料重量x吨之间的函数关系式
；
（2）已知该火箭的起飞重量是544吨 ，是应装载多少吨燃料，才能使该火箭的最大飞行速度达到8km/s，顺利地把飞船发送到预定的轨道？
如图，三棱锥
中，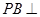
底面ABC于B，
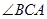=900，
，点E、F分别是PC、AP的中点。
（1）求证：侧面
；
（2）求异面直线AE与BF所成的角；
设F1、F2分别为椭圆C：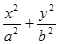
=1（a＞b＞0）的左、右两个焦 点。（1）若椭圆C上的点A（1，
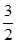）到F1、F2两点的 距离之和等于4，写出椭圆C的方程和焦点坐标；
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程.
已知，如图，AB是⊙O的直径，G为AB延长线上的一点，GCD是⊙O的割线，过点G作AB的垂线，交直线AC于点E，交AD于点F，过G作⊙O的切线，切点为H.求证：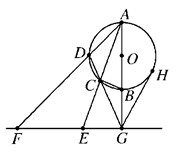
(1)C，D，F，E四点共圆；
(2)GH2＝GE·GF.