已知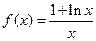 (
(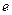 是自然对数的底数,
是自然对数的底数,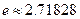 )
)
(1)求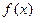 的极大值;
的极大值;
(2)若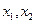 是区间
是区间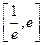 上的任意两个实数,求证:
上的任意两个实数,求证: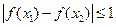 .
.
已知 分别是
分别是 中角
中角 的对边,且
的对边,且 ,
,
⑴求角 的大小;⑵若
的大小;⑵若 ,求
,求 的值.
的值.
若等比数列 的前n项和
的前n项和 ,(1)求实数
,(1)求实数 的值;(2)求数列
的值;(2)求数列 的前n项和
的前n项和 .
.
青年歌手电视大赛共有10名选手参加,并请了7名评委,如图所示的茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,流程图用来编写程序统计每位选手的成绩(各评委所给有效分数的平均值),试根据所给条件回答下列问题:
(1) 根据茎叶图,选手乙的成绩中,众数是多少?选手甲的成绩中,中位数是多少?
(2) 在流程图(如图所示)中,用k表示评委人数,用a表示选手的成绩(各评委所给有效分数的平均值).横线①、②处应填什么?
(3) 根据流程图,甲、乙的成绩分别是多少?
已知 ,(1)求
,(1)求 的值;(2)求
的值;(2)求 的值.
的值.
已知函数
 ,(1) 若
,(1) 若 的解集是
的解集是 ,求实数
,求实数 的值;(2) 若
的值;(2) 若 且
且 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.