如图13所示:宽度L=1m的足够长的U形金属框架水平放置,框架处在竖直向上的匀强磁场中,磁感应强度B=1T,框架导轨上放一根质量m=0.2kg、电阻R=1.0Ω的金属棒ab,棒ab与导轨间的动摩擦因数μ=0.5,现用功率恒为6w的牵引力F使棒从静止开始沿导轨运动(ab棒始终与导轨接触良好且垂直),当棒的电阻R产生热量Q=5.8J时获得稳定速度,此过程中,通过棒的电量q=2.8C(框架电阻不计,g取10m/s2)。问:
(1)ab棒达到的稳定速度多大?
(2)ab棒从静止开始到稳定速度所经历时间是多少?
如图所示,小灯泡规格为“2 V,4 W”,接在光滑水平导轨上,导轨间距为0.1 m,电阻不计.金属棒ab垂直搁在导轨上,电阻为1 Ω,整个装置处于B=1 T的匀强磁场中.求:
(1)为使灯泡正常发光,ab的滑行速度为多大?
(2)拉动金属棒ab的外力的功率有多大?
如图所示,MN、PQ是两条水平放置的平行光滑导轨,其阻值可以忽略不计,轨道间距L=0.6m。匀强磁场垂直导轨平面向下,磁感应强度B=1.0×10-2T,金属杆ab垂直于导轨放置与导轨接触良好,ab杆在导轨间部分的电阻r=1.0Ω,在导轨的左侧连接有电阻R1、R2,阻值分别为R1=3.0Ω, R2=6.0Ω,ab杆在外力作用下以v=5.0m/s的速度向右匀速运动。求:
(1)ab杆哪端的电势高?
(2)求通过ab杆的电流I
(3)求电阻R1上每分钟产生的热量Q。
均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m.将其置于磁感强度为B的水平匀强磁场上方h处,如图20所示.线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界面平行.当cd边刚进入磁场时:
(1)求线框中产生的感应电动势大小.
(2)求cd两点间的电势差大小.
(3)若此时线框加速度恰好为零,求线框下落的高度h所应满足的条件.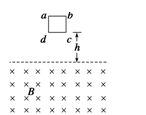
如图19所示,一U形金属框的可动边AC长0.1m,匀强磁场的磁感强度为0.5 T,AC以8 m/s的速度匀速水平向右移动,电阻R为5 Ω,(其它电阻均不计).
(1)计算感应电动势的大小;
(2)求出电阻R中的电流有多大?
如图18所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R=3.0Ω的定值电阻.导体棒ab长l=0.5m,其电阻为r=1.0Ω,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.
⑴ab两点电势差为多少?
⑵使ab棒向右匀速的拉力F为多少?
⑶拉力的功率为多少?