(本小题满分13分)
一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、5,现从盒子中随机抽取卡片。
(I)若从盒子中有 放回地抽取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;
放回地抽取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;
(II)若从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当取到一张记有偶数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望。
在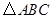 中,内角
中,内角 对边的边长分别是
对边的边长分别是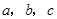 ,已知
,已知 ,
, .
.
(Ⅰ)若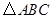 的面积等于
的面积等于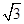 ,求
,求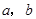 ;
;
(Ⅱ)若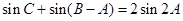 ,求
,求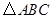 的面积.
的面积.
已知数列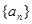 的前
的前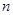 项和
项和 ,数列
,数列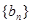 满足
满足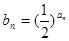
(1)求数列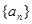 的通项公式
的通项公式 ;(2)求数列
;(2)求数列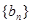 的前
的前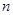 项和
项和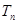 ;
;
(3)求证:不论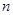 取何正整数,不等式
取何正整数,不等式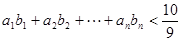 恒成立
恒成立
在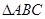 中,三个内角
中,三个内角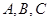 所对的边分别是
所对的边分别是
已知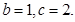
(1)若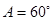 ,求
,求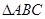 外接圆的半径
外接圆的半径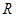
(2)若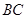 边上的中线长为
边上的中线长为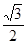 ,求
,求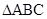 的面积。
的面积。
数列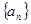 中,
中,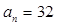 ,
,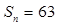 ,
,
(1)若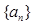 为公差为11的等差数列,求
为公差为11的等差数列,求 ;
;
(2)若 是以
是以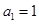 为首项、公比为
为首项、公比为 的等比数列,求
的等比数列,求 的值,并证明对任意
的值,并证明对任意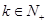 总有:
总有:
已知数列{an}的各项均为正数,前n项的和Sn=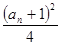
⑴ 求{an}的通项公式;
⑵ 设等比数列{bn}的首项为b,公比为2,前n项的和为Tn.若对任意n∈N*,Sn≤Tn
均成立,求实数b的取值范围.