（本小题满分13分）
如图，已知四棱柱ABCD—A1B1C1D1中，A1D⊥底面ABCD，底面ABCD是边长为1的正方形，侧棱AA1=2。
（I）求证：C1D//平面ABB1A1；
（II）求直线BD1与平面A1C1D所成角的正弦值；
（Ⅲ）求二面角D—A1C1—A的余弦值。
(本小题满分12分)
国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：
序号( ) |
每天睡眠时间 （小时） |
组中值( ) |
频数 |
频率 (  ) |
| 1 |
[4，5) |
4.5 |
8 |
0.04 |
| 2 |
[5，6) |
5.5 |
52 |
0.26 |
| 3 |
[6，7) |
6.5 |
60 |
0.30 |
| 4 |
[7，8) |
7.5 |
56 |
0.28 |
| 5 |
[8，9) |
8.5 |
20 |
0.10 |
| 6 |
[9，10) |
9.5 |
4 |
0.02 |
（Ⅰ）估计每天睡眠时间小于8小时的学生所占的百分比约是多少；
（Ⅱ）该网站利用右边的算法流程图，对样本数据作进一步统计分析，求输出的S的值，并说明S的统计意义.
 |
(本小题满分12分)
设△ABC的三内角A、B、C的对边长分别为a、b、c，已知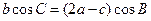
.
（Ⅰ）求角B的大小；
（Ⅱ）若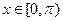
，求函数
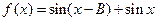的值域.
已知数列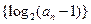
（n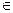
N*）为等差数列，且
，
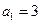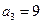．求数列
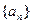的通项公式.
已知数列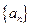
满足
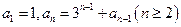,试写出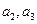
, 并求数列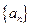的通项公式.
已知递增的等比数列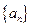
的前三项之积为512,且这三项分别减去1,3,9后又成等差数列,求数列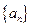的通项公式,并求数列
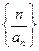的前n项和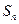
.