已知函数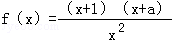 为偶函数
为偶函数
(1)求实数a的值;
(2)当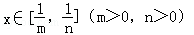 时,若函数f(x)的值域为[2﹣3m,2﹣3n],求m,n的值.
时,若函数f(x)的值域为[2﹣3m,2﹣3n],求m,n的值.
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
已知集合A={x|x2+3x﹣10≤0}
(1)若A⊆B,B={x|m﹣6≤x≤2m+1},求实数m的取值范围;
(2)若B⊆A,B={x|2m﹣1≤x≤m+1},求实数m的取值范围.
化简下列各式(写出化简过程)
(1) ;
;
(2)lg5•lg20+lg22.
设f(x)= 为奇函数,a为常数.
为奇函数,a为常数.
(1)求a的值;并判断f(x)在区间(1,+∞)上的单调性;
(2)若对于区间(3,4)上的每一个x的值,不等式f(x)> 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.