在光滑水平面上有一质量m＝1.0×10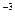
kg、电量q＝1.0×10
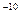C的带正电小球，静止在O点。以O点为原点，在该水平面内建立直角坐标系Oxy。现突然加一沿X轴正方向、场强大小E＝2.0×106V／m的匀强电场，使小球开始运动。经过1.0s，所加电场突然变为沿y轴正方向，场强大小仍为E＝2.0×106V／m的匀强电场。再经过1.0s，所加电场又突然变为另一个匀强电场，使小球在此电场作用下经1.0s速度变为零。求此电场的方向及速度变为零时小球的位置。
一辆汽车正以30m/s的速度在平直路面上行驶，；驾驶员突然发现正前方约50m处有一个障碍物，立即以8m/s2的加速度刹车。为了研究汽车经过2s是否会撞上障碍物，甲、乙两位同学根据已知条件作出以下判断：
甲同学认为汽车已撞上障碍物，理由是：
在2s时间内汽车通过的位移x=vot+
=76m>50m.
乙同学也认为汽车已撞上障碍物，理由是：
在2s时间内汽车通过的位移x=
=56.25m>50m..
问：以上两位同学的判断是否正确？如果正确，给出理由；如果不正确，指出错误的原因，并作出正确的解答。
一物体做匀变速直线运动，从某时刻开始计时，即t=0，在此后连续两个2S内物体通过的位移分别为8m和16m，求
（1）物体的加速度大小。
（2）t=0时物体的速度大小。
某同学为了测定气垫导轨上滑块的加速度，他在滑块上安装了宽度为2cm的遮光板。然后他利用气垫导轨和数值毫秒计记录了遮光板通过第一个光电门所用的时间为Δt1=0.20s,通过第二个光电门的时间Δt2=0.10s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为2.50s,请你根据上面他通过实验得到的数据,
（1）计算出滑块的通过两个光电门的滑块的速度V1和V2.？
（2）计算滑块的加速度？
如图11所示，光滑的水平地面上有一木板，其左端放有一重物，右方有一竖直的墙。重物质量为木板质量的2
倍，重物与木板间的动摩擦因数为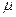
。使木板与重物以共同的速度v0向右运动，某时刻木板与墙发生弹性碰撞，碰撞时间极短。设木板足够长，重物始终在木板上。重力加速度为g。求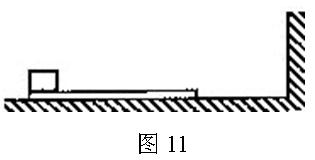
（1）木板第一次与墙碰撞后，重物与木板的共同速度；
（2）木板从第一次与墙碰撞到第二次碰撞所经历的时间;
（3）木板从第一次与墙碰撞开始，整个运动过程所经历的时间。
如图10所示，一条轨道固定在竖直平面内，粗糙的ab段水平，bcde段光滑，cde段是以O为圆心、R为半径的一小段圆弧。可视为质点的物块A和B紧靠在一起，静止于b处，A的质量是B的3倍。两物块在足够大的内力作用下突然分离，分别向左、右始终沿轨道运动。B到d点时速度沿水平方向，此时轨道对B的支持力大小等于B所受重力的3/4，A与ab段的动摩擦因数为μ，重力加速度g，求：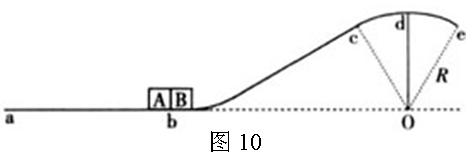
（1）物块B在d点的速度大小;
（2）物块A、B在b点刚分离时，物块B的速度大小；
（3）物块A滑行的最大距离s。