(本小题满分12分)某中学选派 名同学参加上海世博会青年志愿者服务队(简称“青志队”),他们参加活动的次数统计如表所示.
名同学参加上海世博会青年志愿者服务队(简称“青志队”),他们参加活动的次数统计如表所示.
| 活动次数 |
 |
 |
 |
| 参加人数 |
 |
 |
 |
[
(Ⅰ)从“青志队”中任意选 名学生,求这
名学生,求这 名同学中至少有
名同学中至少有 名同学参加活动次数恰好相等的概率;
名同学参加活动次数恰好相等的概率;
(Ⅱ)从“青志队”中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量
的分布列及数学期望 .
.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD是直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,CD= ,平面PAD⊥底面ABCD,若M为AD的中点,E是棱PC上的点.
,平面PAD⊥底面ABCD,若M为AD的中点,E是棱PC上的点.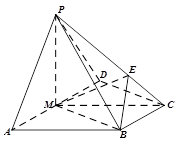
(1)求证:平面EBM⊥平面PAD;
(2)若∠MEC=90°,求三棱锥A-BME的体积.
某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.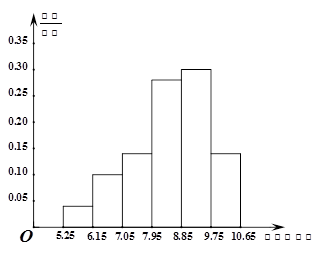
(1)求这次铅球测试成绩合格的人数;
(2)若从第一小组和第二小组中随机抽取两个人的测试成绩,则两个人的测试成绩来自同一小组的概率是多少?
设函数 ,
,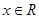 .
.
(1)若 ,求
,求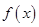 的最大值及相应
的最大值及相应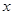 的集合;
的集合;
(2)若 是
是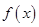 的一个零点,且
的一个零点,且 ,求
,求 的值和
的值和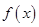 的最小正周期.
的最小正周期.
已知函数
(1)解不等式 ; (2)若不等式
; (2)若不等式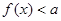 的解集为空集,求实数
的解集为空集,求实数 的取值范围.
的取值范围.
平面直角坐标系中,已知曲线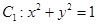 ,将曲线
,将曲线 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的 倍和
倍和 倍后,得到曲线
倍后,得到曲线
(1)试写出曲线 的参数方程;
的参数方程;
(2)在曲线 上求点
上求点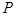 ,使得点
,使得点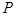 到直线
到直线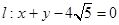 的距离最大,并求距离最大值.
的距离最大,并求距离最大值.