椭圆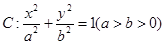 ,作直线
,作直线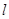 交椭圆于
交椭圆于 两点,
两点, 为线段
为线段 的中点,
的中点, 为坐标原点,设直线
为坐标原点,设直线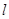 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为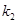 ,
, .
.
(1)求椭圆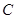 的离心率;
的离心率;
(2)设直线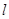 与
与 轴交于点
轴交于点 ,且满足
,且满足 ,当
,当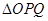 的面积最大时,求椭圆
的面积最大时,求椭圆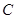 的方程.
的方程.
已知数列{an}的前n项和为
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若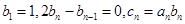 ,求数列{Cn}的前n项和Tn
,求数列{Cn}的前n项和Tn
建造一断面为等腰梯形的防洪堤(如图),梯形的腰与底边所角为60°,考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
已知直线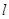 过点
过点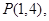
(1)若直线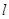 在坐标轴上的截距相等,求直线
在坐标轴上的截距相等,求直线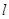 的方程;
的方程;
(2)若直线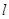 与坐标轴的正半轴相交,求使直线
与坐标轴的正半轴相交,求使直线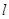 在两坐标轴上的截距之和最小时,直线
在两坐标轴上的截距之和最小时,直线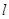 的方程。
的方程。
在△ABC中,角A,B,C所对的边长分别是a,b,c.(1)若sin C + sin(B-A)=" sin" 2A,试判断△ABC的形状;(2)若△ABC的面积S = 3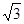 ,且c =
,且c =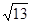 ,C =
,C = ,求a,b的值
,求a,b的值
已知的顶点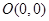 、
、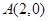 、
、 ,
, 边上的中线所在直线为
边上的中线所在直线为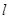 .(1)求
.(1)求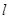 的方程;(2)求点A关于直线
的方程;(2)求点A关于直线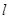 的对称点的坐标。
的对称点的坐标。