建造一断面为等腰梯形的防洪堤(如图),梯形的腰与底边所角为60°,考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
(本小题满分12分)设函数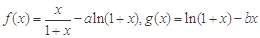 .
.
(1)若函数 在
在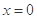 处有极值,求函数
处有极值,求函数 的最大值;
的最大值;
(2)①是否存在实数 ,使得关于
,使得关于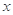 的不等式
的不等式 在
在 上恒成立?若存在,求出
上恒成立?若存在,求出 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式
(本小题满分12分)已知椭圆 的左,右顶点分别为
的左,右顶点分别为 ,圆
,圆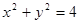 上有一动点
上有一动点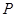 ,点
,点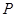 在
在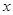 轴的上方,
轴的上方, ,直线
,直线 交椭圆
交椭圆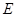 于点
于点 ,连接
,连接 .
.
(1)若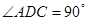 ,求△
,求△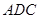 的面积
的面积 ;
;
(2)设直线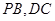 的斜率存在且分别为
的斜率存在且分别为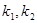 ,若
,若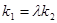 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)如图,在四棱锥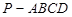 中,平面
中,平面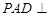 平面
平面 ,
, ,在锐角
,在锐角 中
中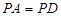 ,并且
,并且 ,
, .
.
(1)点 是
是 上的一点,证明:平面
上的一点,证明:平面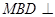 平面
平面 ;
;
(2)若 与平面
与平面 成角
成角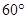 ,当面
,当面 平面
平面 时,求点
时,求点 到平面
到平面 的距离.
的距离.
(本小题满分12分)我国新修订的《环境空气质量标准》指出空气质量指数在 为优秀,各类人群可正常活动.市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
,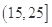 ,
,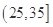 ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
(1)求 的值;
的值;
(2)根据样本数据,试估计这一年度的空气质量指数的平均值;
(3)如果空气质量指数不超过 ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取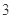 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)“德是”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心(记为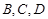 ).当返回舱距地面1万米的
).当返回舱距地面1万米的 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在 点着陆),
点着陆),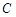 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东 方向,仰角为
方向,仰角为 ,
,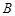 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西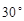 方向,仰角为
方向,仰角为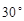 .
. 救援中心测得着陆点
救援中心测得着陆点 位于其正东方向.
位于其正东方向.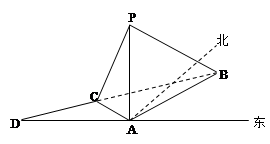
(1)求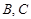 两救援中心间的距离;
两救援中心间的距离;
(2)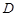 救援中心与着陆点
救援中心与着陆点 间的距离.
间的距离.