(本小题满分12分)我国新修订的《环境空气质量标准》指出空气质量指数在 为优秀,各类人群可正常活动.市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
,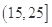 ,
,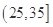 ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
(1)求 的值;
的值;
(2)根据样本数据,试估计这一年度的空气质量指数的平均值;
(3)如果空气质量指数不超过 ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取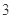 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分14分)
已知函数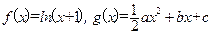 .
.
(1)若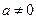 ,曲线
,曲线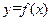 和
和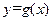 在原点处的切线重合,求实数
在原点处的切线重合,求实数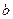 的值.
的值.
(2)若 ,
,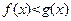 在
在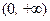 上恒成立,求
上恒成立,求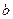 的取值范围.
的取值范围.
(3)函数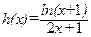 ,在
,在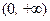 上函数
上函数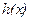 图象与直线y=1是否有交点?若有,求出交点,若没有,请说明理由.
图象与直线y=1是否有交点?若有,求出交点,若没有,请说明理由.
(本小题满分12分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的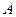 处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以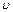 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过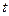 小时与轮船相遇。
小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(本小题满分12分)
曲线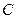 是以原点为中心,以抛物线
是以原点为中心,以抛物线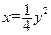 的焦点F为右焦点,离心率为
的焦点F为右焦点,离心率为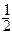 的椭圆,且过F的直线交椭圆C于P、Q两点,M是
的椭圆,且过F的直线交椭圆C于P、Q两点,M是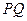 中点.
中点.
(1)求椭圆C的方程;
(2)当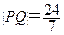 时,求直线PQ的方程.
时,求直线PQ的方程.
(本小题满分12分)
已知数列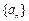 的前n项和
的前n项和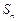 满足:
满足: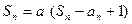 (
(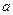 为常数,
为常数,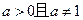 ).
).
(Ⅰ)求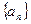 的通项公式;
的通项公式;
(Ⅱ)设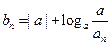 ,若数列
,若数列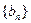 的前n项和
的前n项和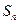 中,
中,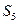 为最大值,求
为最大值,求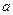 的取值范围.
的取值范围.
(本小题满分12分)
在平面直角坐标系中,点M的坐标为(x,y),点P的坐标为(2,3).
(I)在一个密封的盒子中,放有标号为1,2,3 ,4的三个形状大小完全相同的球,现从此盒中有放回地先后摸取两个球,标号分别记为x、y,求事件“
,4的三个形状大小完全相同的球,现从此盒中有放回地先后摸取两个球,标号分别记为x、y,求事件“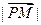 =
=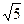 ”的概率;
”的概率;
(II)若利用计算机随机在[0,4]上先后取两个数分别记为x,y,求点M满足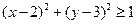 的概率
的概率