设函数 .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)在(1)的条件下,设函数 ,若对于
,若对于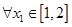 ,
,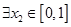 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
如图,在 中,B= ,AC= , 、 两点分别在 、 上.使 , 。现将 沿 折成直二面角,求:

(Ⅰ)异面直线
与
的距离;
(Ⅱ)二面角
的大小(用反三角函数表示).
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.求:
(Ⅰ)打满3局比赛还未停止的概率;
(Ⅱ)比赛停止时已打局数 的分别列与期望 。
设
的内角
的对边分别为
且
.求:
(Ⅰ)
的值;
(Ⅱ) 的值.
备选题:已知函数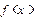 是定义在
是定义在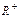 上的减函数,并且满足
上的减函数,并且满足 ,
,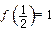 .
.
①求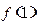 的值;
的值;
②解不等式: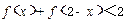 .
.
已知f(x)是定义在[-1,1]上的奇函数. 当a, b∈[-1,1],且a+b≠0时,有
(1)判断函数f(x)的的单调性,并给以证明;
(2)若f(1)=1,且f(x)≤m2-2bm+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数m的取值范围.