(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是矩形,已知AB = 3,AD = 2,PA = 2,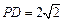 ,
,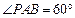 .
.
(1) 证明:AD⊥平面PAB;
(2) 求异面直线PC与AD所成的角的大小;
(3) 求二面角P—BD—A的大小.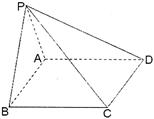
如图所示是某班学生一次数学考试成绩的频率分布直方图,
其中纵轴表示学生数,观察图形,回答下列问题:
(1)全班有多少学生; (2)此次考试平均成绩大概是多少;
(3)不及格的人数有多少?占全班多大比例?
(4)如果80分以上的成绩为优良, 那么这个班的优良率为多少?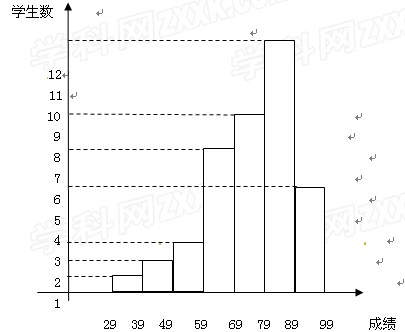
已知直线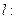
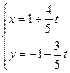 (
(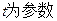 )与曲线C的极坐标方程:
)与曲线C的极坐标方程: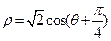 。
。
(1)求直线 与曲线C的直角坐标方程(极点与坐标原点重合,极轴与
与曲线C的直角坐标方程(极点与坐标原点重合,极轴与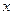 轴重合)
轴重合)
(2)求直线 被曲线C截得的弦长。
被曲线C截得的弦长。
袋中有大小相同的红、黄两种颜色的球各1个,从中任取1只,有放回地抽取3次.求:
(Ⅰ)3只颜色全相同的概率;
(Ⅱ)3只颜色不全相同的概率.
(Ⅲ)若摸到红球时得2分,摸到黄球时得1分,求3次摸球所得总分为5的概率。
若不等式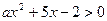 的解集是
的解集是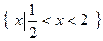 ,求不等式
,求不等式 的解集。
的解集。
已知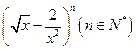 的展开式中,第5项的系数与第3项的系数比是10:1
的展开式中,第5项的系数与第3项的系数比是10:1
求:(1 ) 展开式中含
) 展开式中含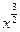 的项
的项
(2) 展开式中二项式系数最大的项
(3) 展开式中系数最大的项