（本小题满分12分）某化妆品生产企业为了占有更多的市场份额，拟在2010年世博会期间进行一系列促销活动，经过市场调查和测算，化妆品的年销量x万件与年促销费t万元之间满足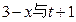
成反比例，如果不搞促销活动，化妆品的年销量只能是1万件，已知2010年生产化妆品的设备折旧、维修等固定费用为3万元，每生产1万件化妆品需要再投入32万元的生产费用，若将每件化妆品的售价定为：其生产成本的150%与平均每件促销费的一半之和，则当年生产的化妆品正好能销完。
（1）将2010年利润y（万元）表示为促销费t（万元）的函数；
（2）该企业2010年的促销费投入多少万元时，企业的年利润最大？
（注：利润=销售收入—生产成本—促销费，生产成本=固定费用+生产费用）
观察下面的程序框图，指出该算法解决的问题.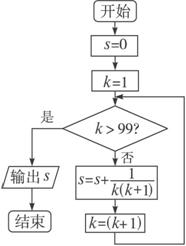 
请用程序框图表示前面讲过的“判断整数n(n＞2)是否为质数”的算法.
这是中国古代的一个著名算法案例：鸡兔49头，100根腿往地里走，问鸡兔各多少？
由相应的程序框图如图，补充完整一个计算1+2+3+…+100的值的算法.（用循环结构）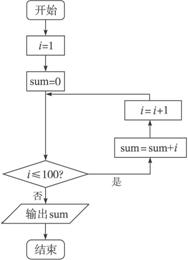 
第一步，设i的值为_____________.
第二步，设sum的值为_____________.
第三步，如果i≤100执行第_____________步,否则，转去执行第_____________步.
第四步，计算sum＋i并将结果代替_____________.
第五步，计算_____________并将结果代替i.
第六步，转去执行第三步.
第七步，输出sum的值并结束算法.
高中某班一共有40名学生，设计算法流程图，统计班级数学成绩良好(分数＞80)和优秀(分数＞90)的人数．