为研究气候的变化趋势,某市气象部门统计了共100个星期中每个星期气温的最高温度和最低温度 ,如下表:
,如下表:
(1)若第六、七、八组的频数 、
、 、
、 为递减的等差数列,且第一组与第八组的频数相同,求出
为递减的等差数列,且第一组与第八组的频数相同,求出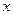 、
、 、
、 、
、 的值;
的值;
(2)若从第一组和第八组的所有星期中随机抽取两个星期,分别记它们的平均温度为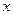 ,
, ,求事件“
,求事件“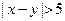 ”的概率.
”的概率.
在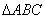 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为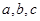 ,且满足
,且满足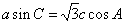 ,
, .
.
(Ⅰ)求角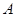 ;(Ⅱ)求
;(Ⅱ)求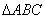 的面积;(Ⅲ)若
的面积;(Ⅲ)若 ,求边
,求边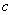 与
与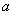 的值.
的值.
已知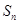 为各项均为正数的等比数列
为各项均为正数的等比数列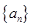 的前n项和,且
的前n项和,且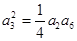 ,
, 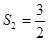
(I)求数列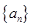 的通项公式;(II)若
的通项公式;(II)若 ,求n的最小值。
,求n的最小值。
已知函数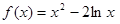 .
.
(Ⅰ)求函数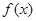 的单调区间;
的单调区间;
(Ⅱ)若存在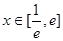 ,使不等式
,使不等式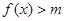 成立,求实数
成立,求实数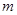 的取值范围;
的取值范围;
(Ⅲ)若关于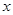 的方程
的方程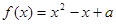 在区间
在区间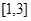 上恰好有两个不相等的实根,求实数
上恰好有两个不相等的实根,求实数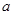 的取值范围.
的取值范围.
已知定义域为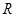 的函数
的函数 是奇函数.
是奇函数.
(Ⅰ)求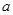 的值;
的值;
(Ⅱ)判断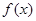 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(Ⅲ)若对任意的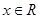 ,不等式
,不等式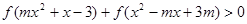 恒成立,求
恒成立,求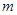 的取值范围.
的取值范围.
某商场销售某件商品的经验表明,该商品每日的销量 (单位:千克)与销售价格
(单位:千克)与销售价格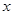 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 ,
,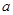 为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
(Ⅰ)求实数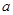 的值;
的值;
(Ⅱ)若该商品的成本为3元/千克,试确定销售价格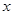 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。