如图所示,位于竖直平面内的光滑轨道,有一段斜的直轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R。一质量为m的小物块从斜轨道上某处由静止开始下滑,然后沿圆形轨道运动。要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过4mg(g为重力加速度)。求物块初始位置相对圆形轨道底部的高度h的取值范围。
如图,半径为R的光滑圆形轨道安置在一竖直平面上,左侧连接一个光滑的弧形轨道,右侧连接动摩擦因数为μ的水平轨道CD.一小球自弧形轨道上端的A处由静止释放,通过圆轨道后,再滑上CD轨道.若在圆轨道最高点B处对轨道的压力恰好为零,到达D点时的速度为 。
。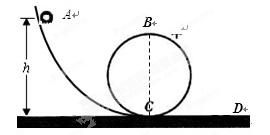
求⑴小球经过B点时速度的大小
⑵小球释放时的高度h
⑶水平轨道CD段的长度l
(12分)如图所示为一物体沿直线运动的x-t图象,根据图象,求:
⑴第2s内的位移,第4s内的位移,前5s的总路程和位移;
⑵各段的速度;
⑶画出对应的v-t图象。
(10分)一个质点沿直线做加速运动,到A点时速度为3m/s,到B点时速度变为12m/s,历时6s;到B点后又做减速运动,再经6s到达C点,并停下来,求:
⑴从A点到B点过程中的加速度;
⑵从B点到C点过程中的加速度。
(6分)汽车从制动到停止下来共用了5s。这段时间内,汽车每1s前进的距离分别是18m、14m、10m、6m、2m。求:
⑴汽车前1s、前2s、前3s、前4s和全程的平均速度;
⑵汽车运动的最后2s的平均速度。
(12分)A、B两辆汽车在笔直的公路上同向行驶。当 B车在A车前84m处时,B车速度为4m/s,且正以2m/s2的加速度做匀加速运动;经过一段时间后,B车加速度突然变为零。A车一直以20m/s的速度做匀速运动。经过12s后两车相遇。求:
⑴B车加速行驶的时间是多少?
⑵两车相遇时B车速度是多少?