解关于实数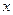 的不等式:
的不等式: 。
。
△ABC的三个内角A、B、C对边分别是a, b, c,且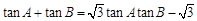 ,
,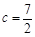 ,又△ABC的面积为
,又△ABC的面积为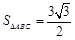 .
.
求:(1)角C;(2)a+b的值.
甲、乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供了两个方面的信息如下图所示。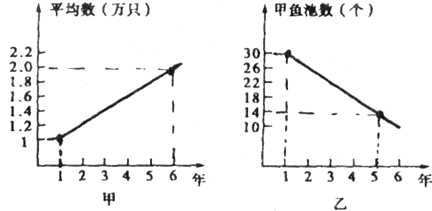
甲调查表明:每个甲鱼池平均出产量从第一年1万只甲鱼上升到第6年2万只。
乙调查表明:甲鱼池个数由第1年30个减少到第6年10个,请你根据提供的信息说明:
(1)第2年甲鱼池的个数及全县出产甲鱼总数;
(2)到第6年这个县的甲鱼养殖业的规模比第1年是扩大了还是缩小了?说明理由;
(3)哪一年的规模最大?说明理由
已知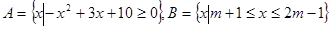 ,若
,若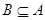 ,求实数
,求实数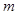 的取值范围.
的取值范围.
已知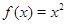 -
-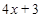 ,求
,求
(1)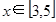 时,
时,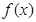 的最值。
的最值。
2. -1,
-1, 时,
时,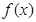 的最值。
的最值。
若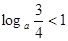
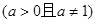 ,求实数
,求实数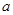 的取值范围。
的取值范围。