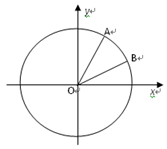
(本小题10分)如图,在平面直角坐标系xoy中,以ox轴为始边做两个锐角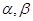 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为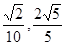
(1)求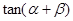 的值; (2)求
的值; (2)求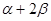 的值。
的值。
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。
(1)求证:CE⊥平面PAD;
(11)若PA=AB=1,AD=3,CD= ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积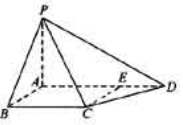
在△ABC中,内角A,B,C的对边分别为a,b,c.已知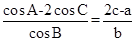 .
.
(1)求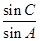 的值;
的值;
(2)若cosB=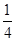 ,△
,△
已知数列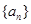 的首项
的首项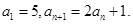
(1)证明:数列 是等比数列;
是等比数列;
(2)若数列 的前n项和为
的前n项和为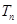 ,试比较
,试比较 与
与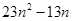 的大小。
的大小。
设动点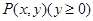 到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C。
到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C。
(1)求点P的轨迹方程;
(2)若圆心在曲线C上的动圆M过点A(0,2),试证明圆M与x轴必相交,且截x轴所得的弦长为定值。
设函数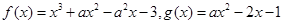 ,其中实数
,其中实数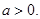
(1)求函数 的单调区间;
的单调区间;
(2)若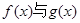 在区间
在区间 上均为增函数,求a的取值范围。
上均为增函数,求a的取值范围。